Higgs

The is a directed follower social network from Twitter, in the context of the announcement of the discovery of a particle with the features of Higgs boson. The network contains loops.

Metadata

CodeHI
Internal namehiggs-twitter-social
NameHiggs
Data sourcehttp://snap.stanford.edu/data/higgs-twitter.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Online social network
Dataset timestamp 2012-07-01 ⋯ 2012-07-07
Node meaningUser
Edge meaningFollow
Network formatUnipartite, directed
Edge typeUnweighted, no multiple edges
ReciprocalContains reciprocal edges
Directed cyclesContains directed cycles
LoopsContains loops
Snapshot Is a snapshot and likely to not contain all data

Statistics

Size n =456,626
Volume m =14,855,842
Loop count l =23
Wedge count s =28,786,965,703
Claw count z =228,329,313,547,960
Cross count x =1,978,606,030,373,039,872
Triangle count t =83,023,401
Square count q =54,010,191,351
4-Tour count T4 =547,254,410,446
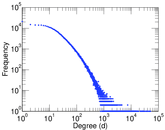
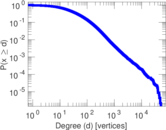
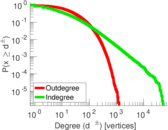
Maximum degree dmax =51,388
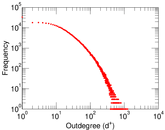
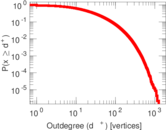
Maximum outdegree d+max =1,259
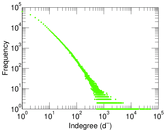
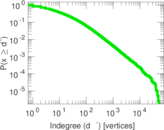
Maximum indegree d−max =51,386
Average degree d =65.067 9
Fill p =7.124 85 × 10−5
Size of LCC N =456,290
Size of LSCC Ns =360,210
Relative size of LSCC Nrs =0.788 851
Diameter δ =12
50-Percentile effective diameter δ0.5 =2.639 63
90-Percentile effective diameter δ0.9 =3.706 21
Median distance δM =3
Mean distance δm =3.174 10
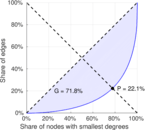
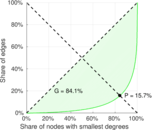
Gini coefficient G =0.717 584
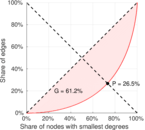
Balanced inequality ratio P =0.220 890
Outdegree balanced inequality ratio P+ =0.265 009
Indegree balanced inequality ratio P− =0.156 805
Relative edge distribution entropy Her =0.897 103
Power law exponent γ =1.346 90
Tail power law exponent γt =2.271 00
Tail power law exponent with p γ3 =2.271 00
p-value p =0.000 00
Outdegree tail power law exponent with p γ3,o =2.671 00
Outdegree p-value po =0.000 00
Indegree tail power law exponent with p γ3,i =2.051 00
Indegree p-value pi =0.000 00
Degree assortativity ρ =−0.098 444 8
Degree assortativity p-value pρ =0.000 00
In/outdegree correlation ρ± =+0.688 659
Clustering coefficient c =0.008 652 19
Directed clustering coefficient c± =0.100 511
Spectral norm α =677.185
Operator 2-norm ν =608.347
Cyclic eigenvalue π =202.697
Reciprocity y =0.316 026
Non-bipartivity bA =0.169 817
Normalized non-bipartivity bN =0.054 334 1
Algebraic non-bipartivity χ =0.091 225 0
Spectral bipartite frustration bK =0.000 415 976

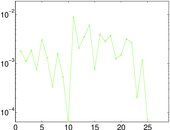
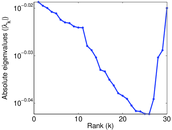
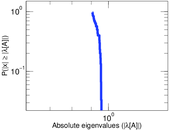
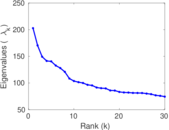
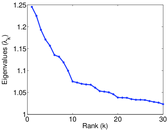
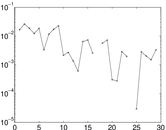
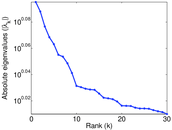
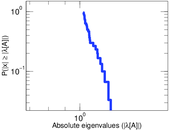
Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Hop distribution

In/outdegree scatter plot

Clustering coefficient distribution

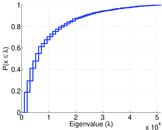
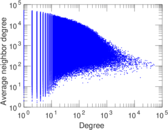
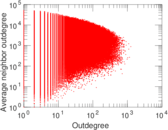
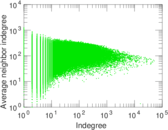
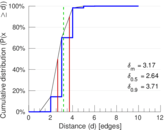
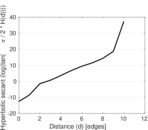
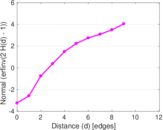
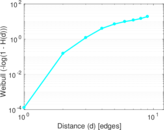
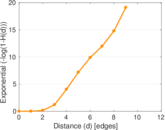
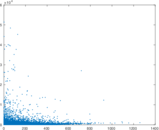
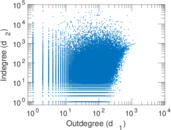
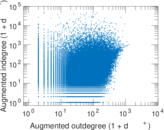
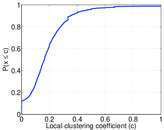
Matrix decompositions plots

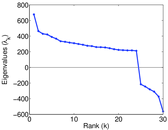
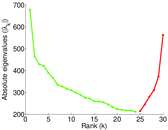
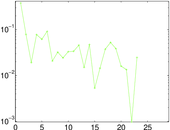
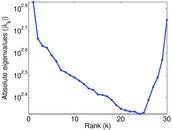
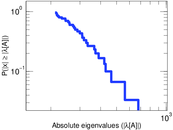
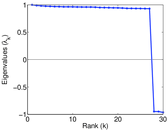
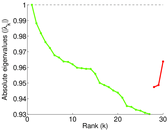
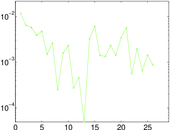
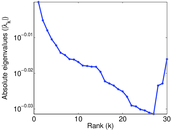
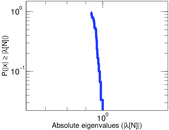
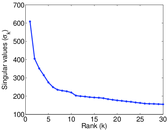
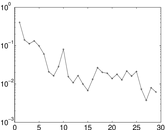
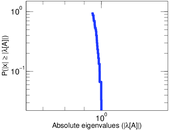
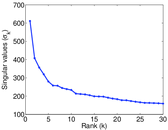
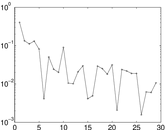
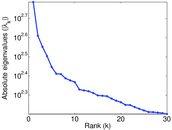
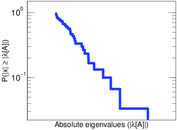
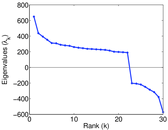
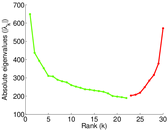
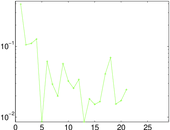
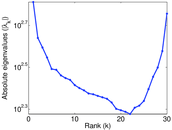
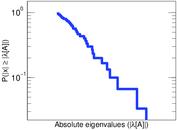
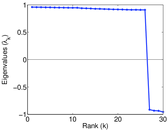
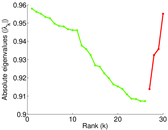
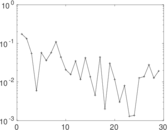
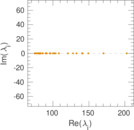
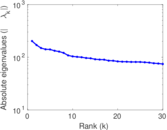
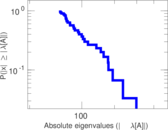
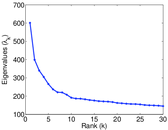
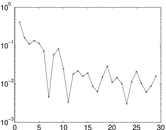
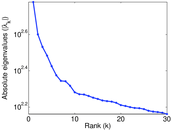
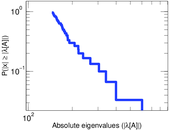
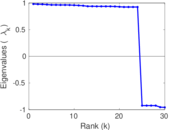
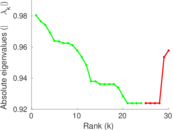
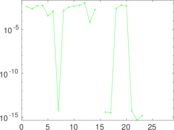
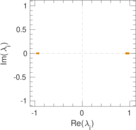
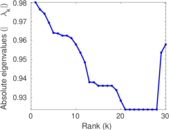
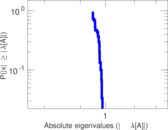
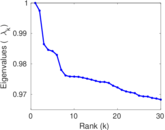
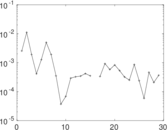
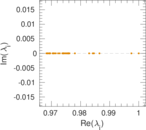
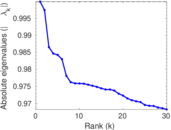
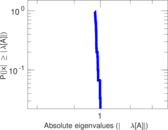
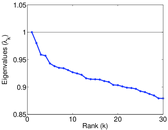
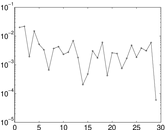
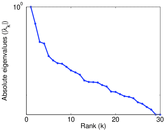
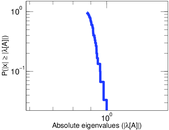
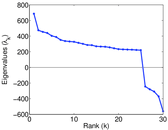
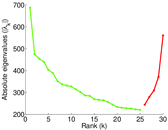
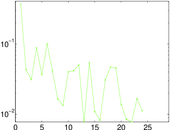
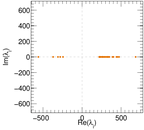
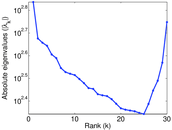
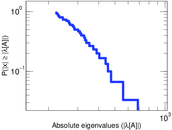
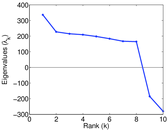
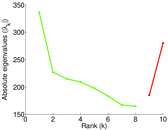
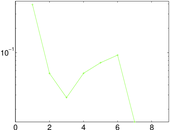
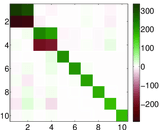
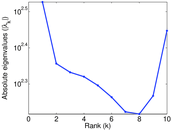
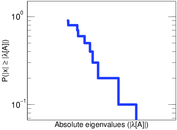
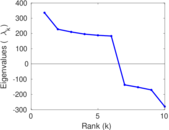
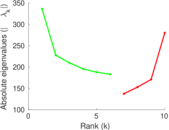
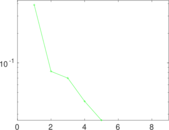
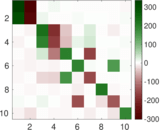
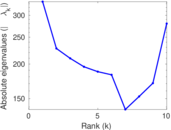
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Jure Leskovec. Stanford Network Analysis Project. http://snap.stanford.edu/, September 2014.