Pokec

This is the friendship network from the Slovak social network Pokec. Nodes are users of Pokec and directed edges represent friendships.

Metadata

CodePL
Internal namesoc-pokec-relationships
NamePokec
Data sourcehttp://snap.stanford.edu/data/soc-pokec.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Online social network
Node meaningUser
Edge meaningFriendship
Network formatUnipartite, directed
Edge typeUnweighted, no multiple edges
ReciprocalContains reciprocal edges
Directed cyclesContains directed cycles
LoopsDoes not contain loops

Statistics

Size n =1,632,803
Volume m =30,622,564
Loop count l =0
Wedge count s =2,086,073,558
Claw count z =3,352,153,545,587
Cross count x =13,577,672,765,395,898
Triangle count t =32,557,458
Square count q =953,891,791
Maximum degree dmax =20,518
Maximum outdegree d+max =8,763
Maximum indegree d−max =13,733
Average degree d =37.509 2
Fill p =1.148 61 × 10−5
Size of LCC N =1,632,803
Size of LSCC Ns =1,304,537
Relative size of LSCC Nrs =0.798 956
Diameter δ =14
50-Percentile effective diameter δ0.5 =4.175 49
90-Percentile effective diameter δ0.9 =5.109 52
Median distance δM =5
Mean distance δm =4.657 78
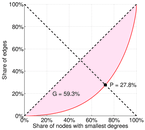
Gini coefficient G =0.620 519
Balanced inequality ratio P =0.263 488
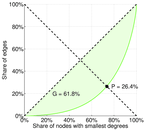
Outdegree balanced inequality ratio P+ =0.277 918
Indegree balanced inequality ratio P− =0.263 811
Relative edge distribution entropy Her =0.951 356
Power law exponent γ =1.404 80
Tail power law exponent γt =3.061 00
Degree assortativity ρ =+0.001 636 60
Degree assortativity p-value pρ =8.265 56 × 10−28
Clustering coefficient c =0.046 821 2
Directed clustering coefficient c± =0.054 413 4
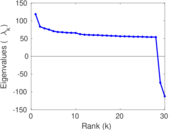
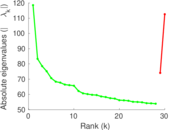
Spectral norm α =247.819
Operator 2-norm ν =132.219
Cyclic eigenvalue π =118.527
Reciprocity y =0.543 429
Non-bipartivity bA =0.049 025 9
Normalized non-bipartivity bN =0.012 475 3

Plots

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the normalized adjacency matrix

Hop distribution

In/outdegree scatter plot

SynGraphy

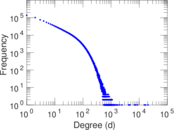
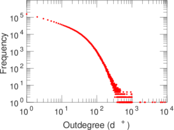
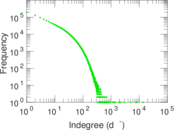
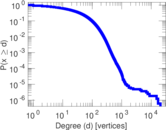
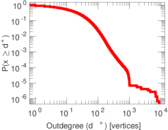
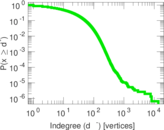
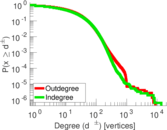
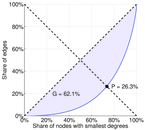
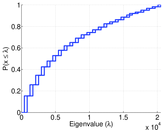
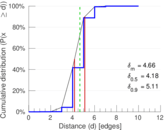
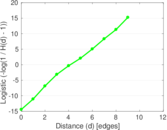
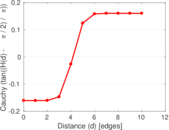
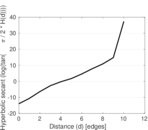
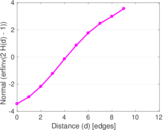
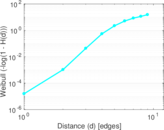
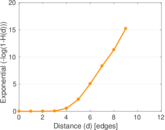
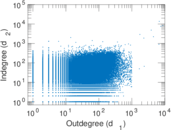
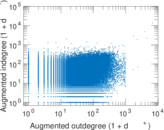
Matrix decompositions plots

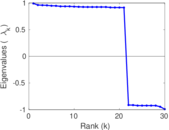
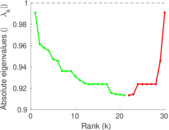
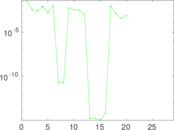
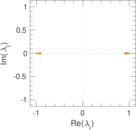
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Lubos Takac and Michal Zabovsky. Data analysis in public social networks. In Proc. Int. Scientific Conf. and Int. Workshop Present Day Trends of Innovations, 2012.