Berkeley/Stanford
This is the hyperlink network of the websites of the Universities in Berkley
and Stanford. Nodes represent web pages, and directed edges represent
hyperlinks.
Metadata
Statistics
| Size | n = | 685,230
|
| Volume | m = | 7,600,595
|
| Loop count | l = | 0
|
| Wedge count | s = | 27,982,987,280
|
| Claw count | z = | 383,198,935,132,861
|
| Cross count | x = | 4,925,431,856,926,247,936
|
| Triangle count | t = | 64,690,980
|
| Square count | q = | 127,118,333,411
|
| 4-Tour count | T4 = | 1,128,891,915,348
|
| Maximum degree | dmax = | 84,290
|
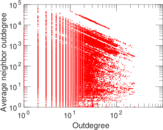
| Maximum outdegree | d+max = | 249
|
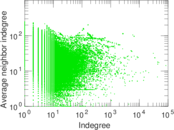
| Maximum indegree | d−max = | 84,208
|
| Average degree | d = | 22.184 1
|
| Fill | p = | 1.618 73 × 10−5
|
| Size of LCC | N = | 654,782
|
| Size of LSCC | Ns = | 334,857
|
| Relative size of LSCC | Nrs = | 0.488 678
|
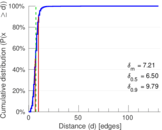
| Diameter | δ = | 208
|
| 50-Percentile effective diameter | δ0.5 = | 6.501 42
|
| 90-Percentile effective diameter | δ0.9 = | 9.788 90
|
| Median distance | δM = | 7
|
| Mean distance | δm = | 7.211 72
|
| Gini coefficient | G = | 0.659 006
|
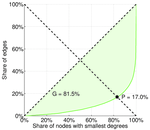
| Balanced inequality ratio | P = | 0.250 475
|
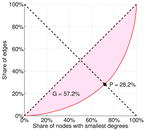
| Outdegree balanced inequality ratio | P+ = | 0.282 235
|
| Indegree balanced inequality ratio | P− = | 0.169 903
|
| Relative edge distribution entropy | Her = | 0.886 433
|
| Power law exponent | γ = | 1.486 07
|
| Tail power law exponent | γt = | 2.601 00
|
| Tail power law exponent with p | γ3 = | 2.601 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 2.091 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 1.971 00
|
| Indegree p-value | pi = | 0.000 00
|
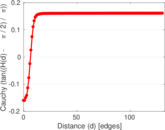
| Degree assortativity | ρ = | −0.112 728
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.313 250
|
| Clustering coefficient | c = | 0.006 935 39
|
| Directed clustering coefficient | c± = | 0.595 513
|
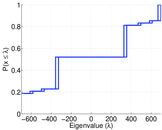
| Spectral norm | α = | 697.551
|
| Operator 2-norm | ν = | 674.675
|
| Cyclic eigenvalue | π = | 162.347
|
| Algebraic connectivity | a = | 2.784 94 × 10−5
|
| Reciprocity | y = | 0.250 276
|
| Non-bipartivity | bA = | 0.058 559 0
|
| Normalized non-bipartivity | bN = | 0.000 201 474
|
| Spectral bipartite frustration | bK = | 1.644 81 × 10−5
|
| Controllability | C = | 271,368
|
| Relative controllability | Cr = | 0.396 025
|
Plots
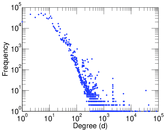
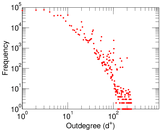
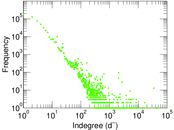
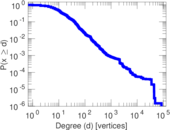
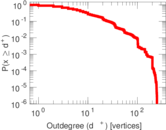
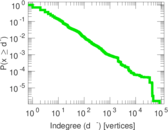
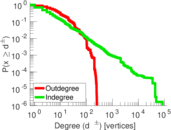
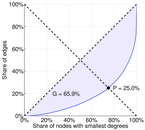
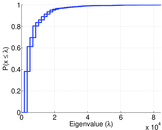

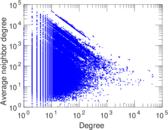

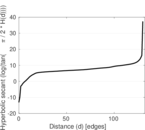
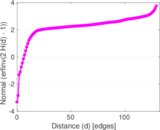
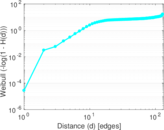
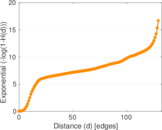
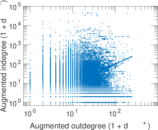
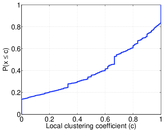
Matrix decompositions plots
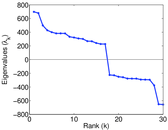
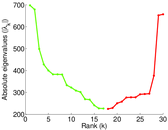
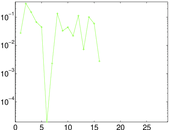
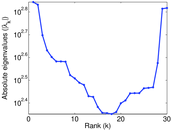
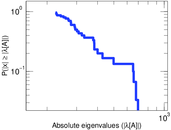
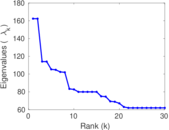
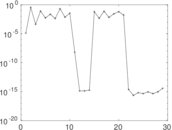
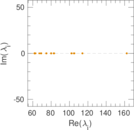
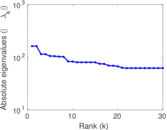
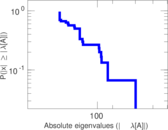
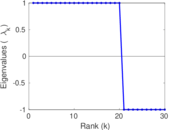
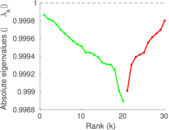
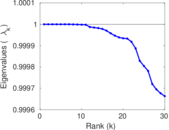
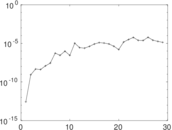
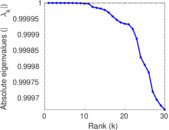
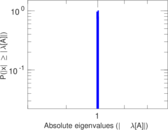
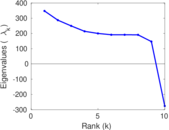
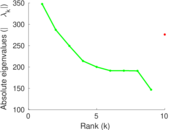
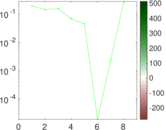

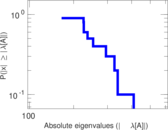
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Jure Leskovec, Kevin J. Lang, Anirban Dasgupta, and Michael W. Mahoney.
Statistical properties of community structure in large social and
information networks.
In Proc. Int. World Wide Web Conf., pages 695–704, 2008.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee






















































