Google hyperlinks
This is a network of web pages connected by hyperlinks. The data was released
in 2002 by Google as a part of the Google Programming Contest.
Metadata
Statistics
| Size | n = | 875,713
|
| Volume | m = | 5,105,039
|
| Loop count | l = | 0
|
| Wedge count | s = | 727,417,224
|
| Claw count | z = | 667,827,082,809
|
| Cross count | x = | 649,372,878,638,139
|
| Triangle count | t = | 13,391,903
|
| Square count | q = | 539,575,204
|
| 4-Tour count | T4 = | 7,234,914,630
|
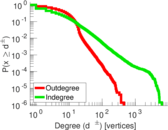
| Maximum degree | dmax = | 6,353
|
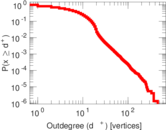
| Maximum outdegree | d+max = | 456
|
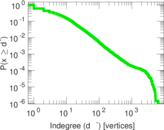
| Maximum indegree | d−max = | 6,326
|
| Average degree | d = | 11.659 2
|
| Fill | p = | 6.656 96 × 10−6
|
| Size of LCC | N = | 855,802
|
| Size of LSCC | Ns = | 434,818
|
| Relative size of LSCC | Nrs = | 0.496 530
|
| Diameter | δ = | 24
|
| 50-Percentile effective diameter | δ0.5 = | 5.742 34
|
| 90-Percentile effective diameter | δ0.9 = | 7.948 20
|
| Median distance | δM = | 6
|
| Mean distance | δm = | 6.373 75
|
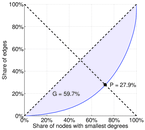
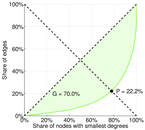
| Gini coefficient | G = | 0.597 285
|
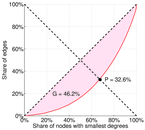
| Balanced inequality ratio | P = | 0.279 274
|
| Outdegree balanced inequality ratio | P+ = | 0.325 541
|
| Indegree balanced inequality ratio | P− = | 0.221 834
|
| Relative edge distribution entropy | Her = | 0.941 199
|
| Power law exponent | γ = | 1.617 21
|
| Tail power law exponent | γt = | 2.731 00
|
| Tail power law exponent with p | γ3 = | 2.731 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 3.661 00
|
| Outdegree p-value | po = | 0.300 000
|
| Indegree tail power law exponent with p | γ3,i = | 2.571 00
|
| Indegree p-value | pi = | 0.000 00
|
| Degree assortativity | ρ = | −0.055 089 0
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.388 241
|
| Clustering coefficient | c = | 0.055 230 6
|
| Directed clustering coefficient | c± = | 0.476 963
|
| Spectral norm | α = | 116.964
|
| Operator 2-norm | ν = | 105.911
|
| Cyclic eigenvalue | π = | 37.639 6
|
| Algebraic connectivity | a = | 0.002 704 91
|
| Reciprocity | y = | 0.306 751
|
| Non-bipartivity | bA = | 0.174 111
|
| Normalized non-bipartivity | bN = | 0.001 246 93
|
| Spectral bipartite frustration | bK = | 9.439 92 × 10−5
|
| Controllability | C = | 426,073
|
| Relative controllability | Cr = | 0.486 544
|
Plots
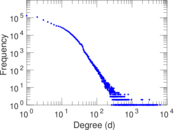
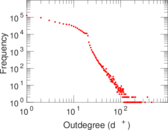
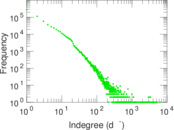
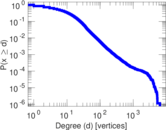
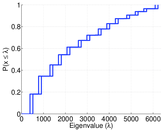
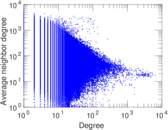
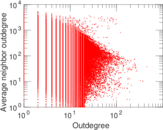
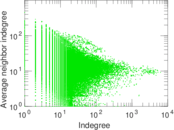
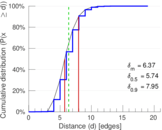
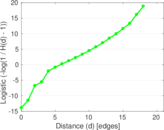
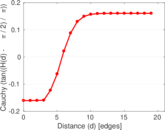
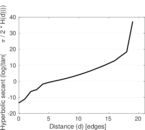
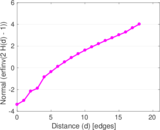
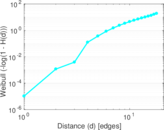
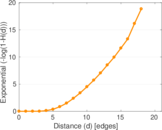
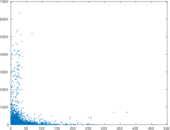
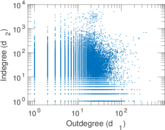
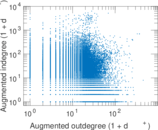
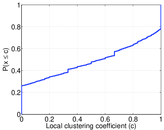
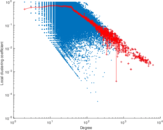
Matrix decompositions plots
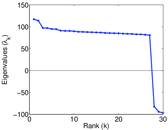
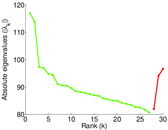
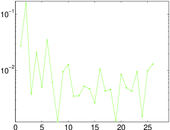
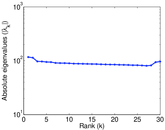
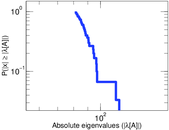
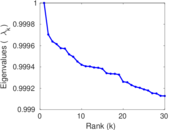
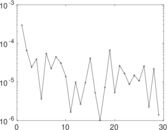
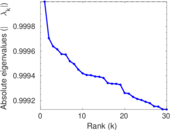
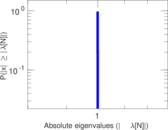
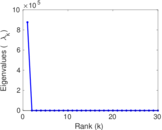
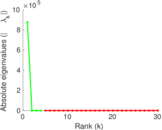
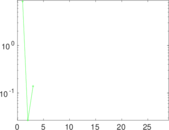
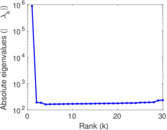
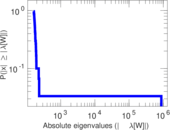
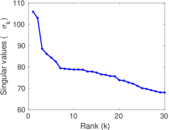
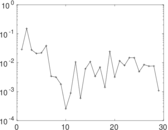
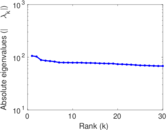
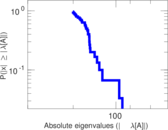
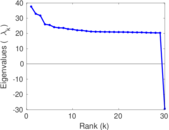
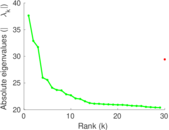
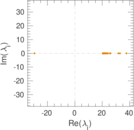
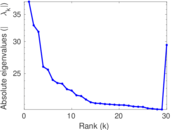
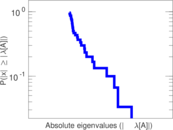
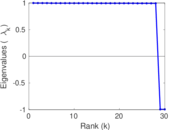
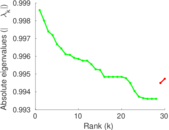
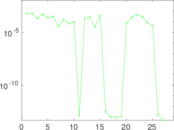
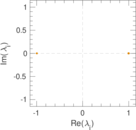
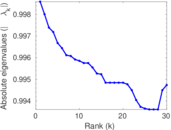
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Jure Leskovec, Kevin J. Lang, Anirban Dasgupta, and Michael W. Mahoney.
Statistical properties of community structure in large social and
information networks.
In Proc. Int. World Wide Web Conf., pages 695–704, 2008.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee




























































