Wikipedia links (sq)

This network consists of the wikilinks of the Wikipedia in the Albanian language (sq). Nodes are Wikipedia articles, and directed edges are wikilinks, i.e., hyperlinks within one wiki. In the wiki source, these are indicated with [[double brackets]]. Only pages in the article namespace are included.

Metadata

CodeWsq
Internal namewikipedia_link_sq
NameWikipedia links (sq)
Data sourcehttp://dumps.wikimedia.org/
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Hyperlink network
Node meaningArticle
Edge meaningWikilink
Network formatUnipartite, directed
Edge typeUnweighted, no multiple edges
ReciprocalContains reciprocal edges
Directed cyclesContains directed cycles
LoopsContains loops

Statistics

Size n =97,940
Volume m =2,491,433
Loop count l =120
Wedge count s =1,637,254,072
Cross count x =31,163,634,202,548,320
Triangle count t =46,254,313
Square count q =11,035,437,550
4-Tour count T4 =94,835,957,018
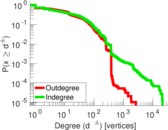
Maximum degree dmax =21,524
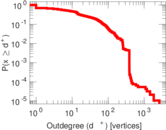
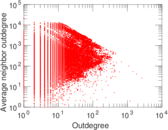
Maximum outdegree d+max =2,638
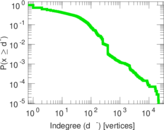
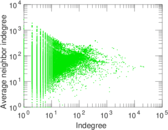
Maximum indegree d−max =21,515
Average degree d =50.876 7
Fill p =0.000 259 734
Size of LCC N =97,071
Size of LSCC Ns =58,688
Relative size of LSCC Nrs =0.599 224
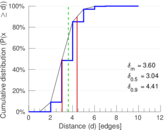
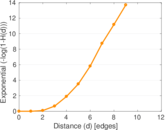
Diameter δ =12
50-Percentile effective diameter δ0.5 =3.039 56
90-Percentile effective diameter δ0.9 =4.407 89
Median distance δM =4
Mean distance δm =3.604 53
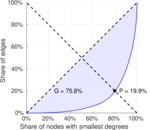
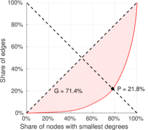
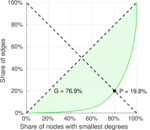
Balanced inequality ratio P =0.199 269
Outdegree balanced inequality ratio P+ =0.218 337
Indegree balanced inequality ratio P− =0.197 777
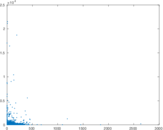
Power law exponent γ =1.433 27
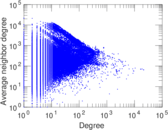
Degree assortativity ρ =−0.071 927 4
Degree assortativity p-value pρ =0.000 00
In/outdegree correlation ρ± =+0.692 406
Clustering coefficient c =0.084 753 5
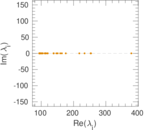
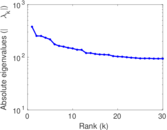
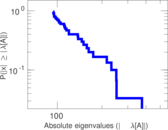
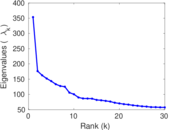
Operator 2-norm ν =383.077
Cyclic eigenvalue π =379.005
Non-bipartivity bA =0.560 155
Normalized non-bipartivity bN =0.023 987 3
Algebraic non-bipartivity χ =0.071 788 1
Spectral bipartite frustration bK =0.000 506 492
Controllability C =42,365
Relative controllability Cr =0.432 561

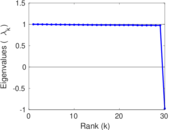
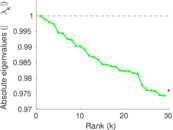
Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral graph drawing based on the Laplacian

Degree assortativity

Hop distribution

Delaunay graph drawing

In/outdegree scatter plot

SynGraphy

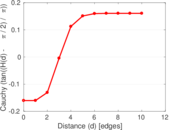
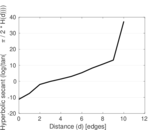
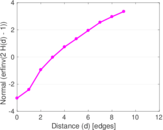
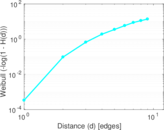
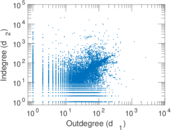
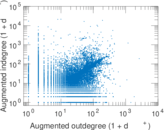
Matrix decompositions plots

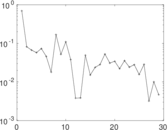
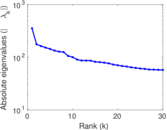
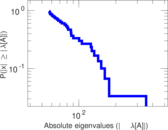
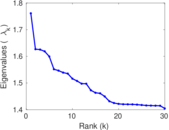
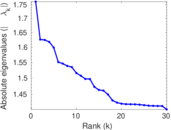
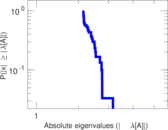
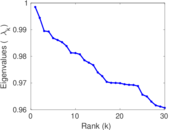
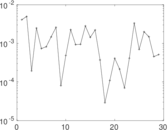
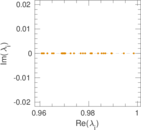
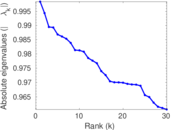
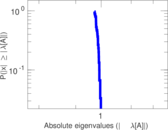
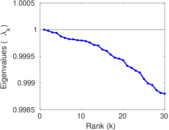
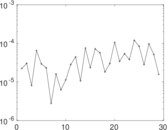
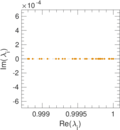
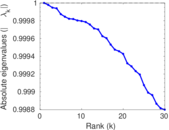
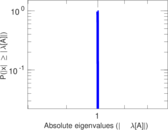
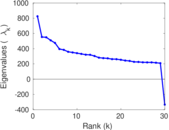
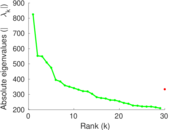
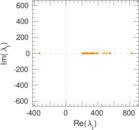
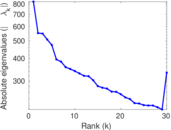
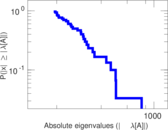
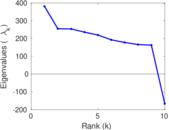
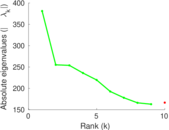
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]