Hudong internal
This is the directed network of hyperlinks between the articles of the Chinese
online encyclopedia Hudong (互动百科, http://www.hudong.com/).
Metadata
Statistics
| Size | n = | 1,984,484
|
| Volume | m = | 14,869,484
|
| Loop count | l = | 187,226
|
| Wedge count | s = | 18,725,710,519
|
| Claw count | z = | 119,274,873,657,963
|
| Cross count | x = | 1,151,551,426,720,799,744
|
| Triangle count | t = | 21,618,971
|
| Square count | q = | 7,069,486,215
|
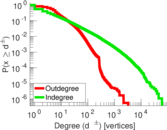
| Maximum degree | dmax = | 61,572
|
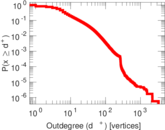
| Maximum outdegree | d+max = | 3,296
|
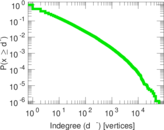
| Maximum indegree | d−max = | 61,227
|
| Average degree | d = | 14.985 7
|
| Fill | p = | 3.775 73 × 10−6
|
| Size of LCC | N = | 1,962,418
|
| Size of LSCC | Ns = | 365,558
|
| Relative size of LSCC | Nrs = | 0.184 208
|
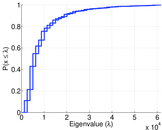
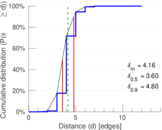
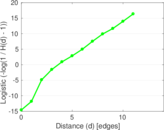
| Diameter | δ = | 16
|
| 50-Percentile effective diameter | δ0.5 = | 3.600 06
|
| 90-Percentile effective diameter | δ0.9 = | 4.802 48
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 4.162 82
|
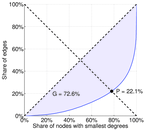
| Gini coefficient | G = | 0.725 545
|
| Balanced inequality ratio | P = | 0.221 195
|
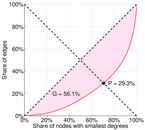
| Outdegree balanced inequality ratio | P+ = | 0.293 156
|
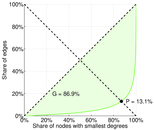
| Indegree balanced inequality ratio | P− = | 0.130 624
|
| Relative edge distribution entropy | Her = | 0.881 589
|
| Power law exponent | γ = | 1.613 37
|
| Tail power law exponent | γt = | 2.301 00
|
| Degree assortativity | ρ = | −0.067 814 2
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| Clustering coefficient | c = | 0.003 463 52
|
| Directed clustering coefficient | c± = | 0.104 624
|
| Spectral norm | α = | 558.805
|
| Operator 2-norm | ν = | 314.852
|
| Cyclic eigenvalue | π = | 265.004
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.116 98
|
| Reciprocity | y = | 0.046 738 5
|
| Non-bipartivity | bA = | 0.467 526
|
| Normalized non-bipartivity | bN = | 0.000 913 442
|
| Algebraic non-bipartivity | χ = | 0.001 825 86
|
| Spectral bipartite frustration | bK = | 3.068 41 × 10−5
|
Plots
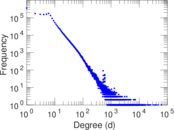
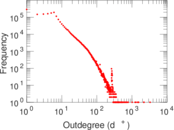
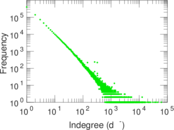
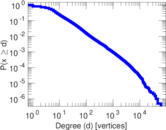
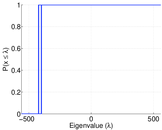
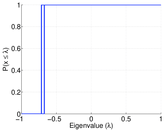


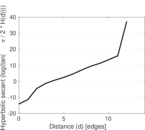
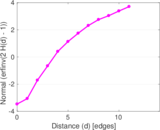
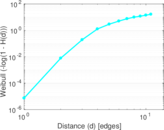
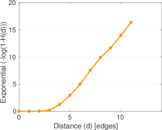
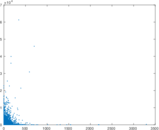
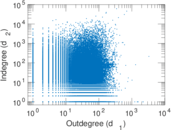
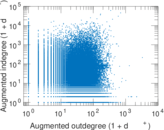
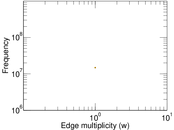
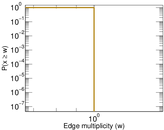
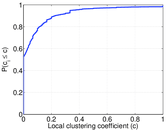
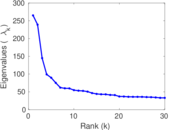
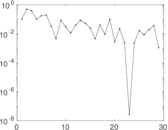
Matrix decompositions plots
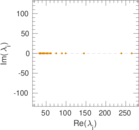
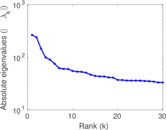
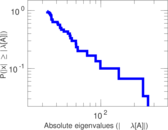
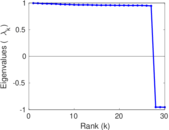
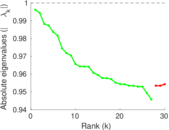
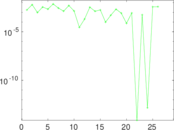
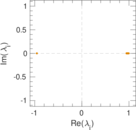
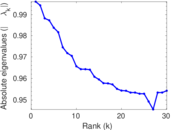
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Xing Niu, Xinruo Sun, Haofen Wang, Shu Rong, Guilin Qi, and Yong Yu.
Zhishi.me – weaving Chinese linking open data.
In Proc. Int. Semant. Web Conf., pages 205–220, 2011.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee






































