CAIDA

This is the undirected network of autonomous systems of the Internet connected with each other from the CAIDA project, collected in 2007. Nodes are autonomous systems (AS), and edges denote communication.

Metadata

CodeIN
Internal nameas-caida20071105
NameCAIDA
Data sourcehttp://snap.stanford.edu/data/as-caida.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Computer network
Node meaningAutonomous system
Edge meaningCommunication
Network formatUnipartite, undirected
Edge typeUnweighted, no multiple edges
LoopsDoes not contain loops
Orientation Is not directed, but the underlying data is

Statistics

Size n =26,475
Volume m =53,381
Loop count l =0
Wedge count s =14,906,270
Claw count z =7,839,606,991
Cross count x =3,916,793,044,776
Triangle count t =36,365
Square count q =2,287,349
4-Tour count T4 =78,030,634
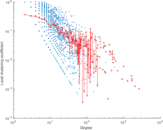
Maximum degree dmax =2,628
Average degree d =4.032 56
Fill p =0.000 152 321
Size of LCC N =26,475
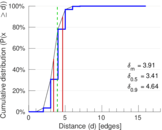
Diameter δ =17
50-Percentile effective diameter δ0.5 =3.407 07
90-Percentile effective diameter δ0.9 =4.636 96
Median distance δM =4
Mean distance δm =3.912 47
Gini coefficient G =0.628 058
Balanced inequality ratio P =0.268 963
Relative edge distribution entropy Her =0.838 051
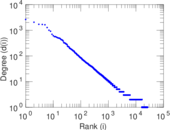
Power law exponent γ =2.508 65
Tail power law exponent γt =2.091 00
Tail power law exponent with p γ3 =2.091 00
p-value p =0.733 000
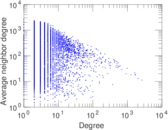
Degree assortativity ρ =−0.194 646
Degree assortativity p-value pρ =0.000 00
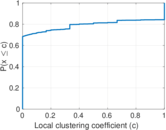
Clustering coefficient c =0.007 318 73
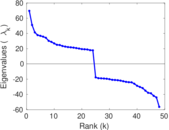
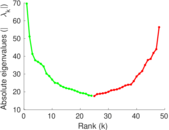
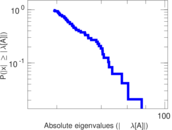
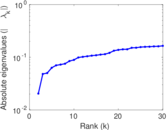
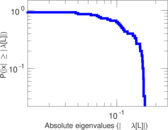
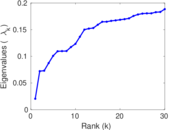
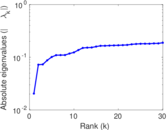
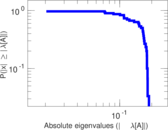
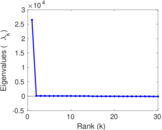
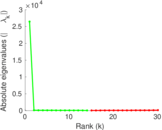
Spectral norm α =69.643 4
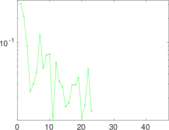
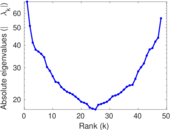
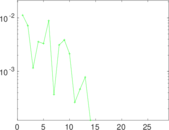
Algebraic connectivity a =0.020 436 8
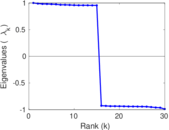
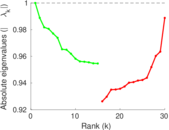
Spectral separation |λ1[A] / λ2[A]| =1.235 74
Non-bipartivity bA =0.190 767
Normalized non-bipartivity bN =0.011 209 8
Algebraic non-bipartivity χ =0.020 451 8
Spectral bipartite frustration bK =0.001 267 92
Controllability C =19,127
Relative controllability Cr =0.722 455

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

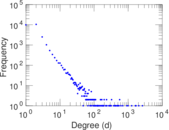
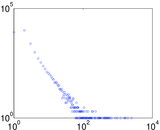
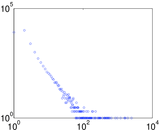
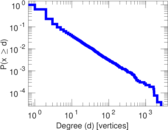
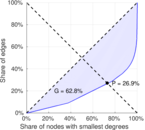
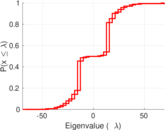
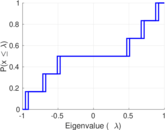
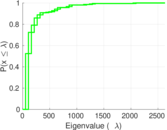
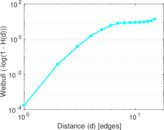
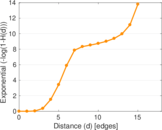
Matrix decompositions plots

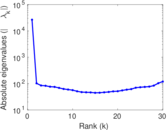
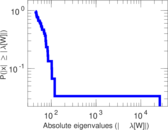
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Jure Leskovec, Jon Kleinberg, and Christos Faloutsos. Graph evolution: Densification and shrinking diameters. ACM Trans. Knowl. Discov. from Data, 1(1):1–40, 2007.