Route views

This is the undirected network of autonomous systems of the Internet connected with each other. Nodes are autonomous systems (AS), and edges denote communitation. The network contains loops.

Metadata

CodeAS
Internal nameas20000102
NameRoute views
Data sourcehttp://snap.stanford.edu/data/as.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Computer network
Node meaningAutonomous system
Edge meaningCommunication
Network formatUnipartite, undirected
Edge typeUnweighted, no multiple edges
LoopsContains loops
Orientation Is not directed, but the underlying data is

Statistics

Size n =6,474
Volume m =13,895
Loop count l =1,323
Wedge count s =2,059,364
Claw count z =674,974,421
Cross count x =212,651,094,228
Triangle count t =6,584
Square count q =288,840
4-Tour count T4 =10,573,320
Maximum degree dmax =1,459
Average degree d =4.292 55
Fill p =0.000 662 943
Size of LCC N =6,474
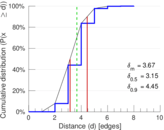
Diameter δ =9
50-Percentile effective diameter δ0.5 =3.148 22
90-Percentile effective diameter δ0.9 =4.449 21
Median distance δM =4
Mean distance δm =3.666 86
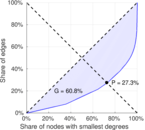
Gini coefficient G =0.608 189
Balanced inequality ratio P =0.273 480
Relative edge distribution entropy Her =0.853 888
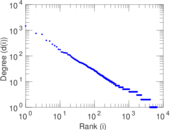
Power law exponent γ =2.336 32
Tail power law exponent γt =2.111 00
Tail power law exponent with p γ3 =2.111 00
p-value p =0.291 000
Degree assortativity ρ =−0.181 755
Degree assortativity p-value pρ =1.098 82 × 10−185
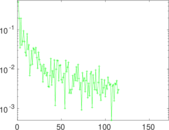
Clustering coefficient c =0.009 591 31
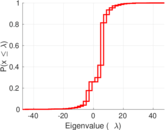
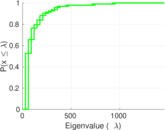
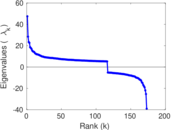
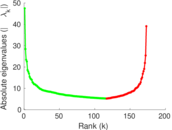
Spectral norm α =47.476 6
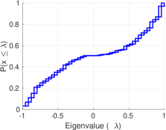
Algebraic connectivity a =0.088 030 8
Spectral separation |λ1[A] / λ2[A]| =1.214 21
Non-bipartivity bA =0.176 419
Normalized non-bipartivity bN =0.045 798 5
Algebraic non-bipartivity χ =0.089 770 8
Spectral bipartite frustration bK =0.005 228 29
Controllability C =3,605
Relative controllability Cr =0.556 843

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

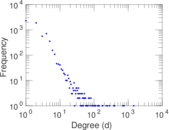
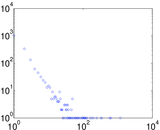
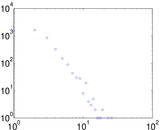
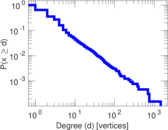
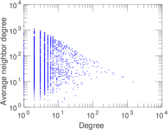
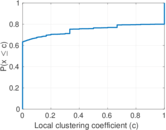
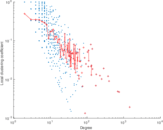
Matrix decompositions plots

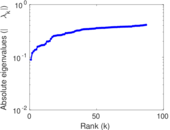
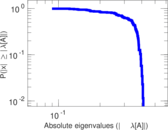
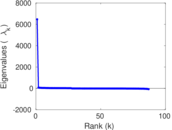
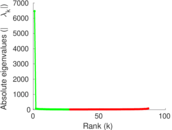
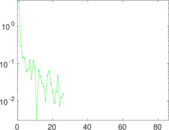
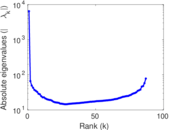
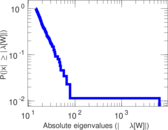
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Jure Leskovec, Jon Kleinberg, and Christos Faloutsos. Graph evolution: Densification and shrinking diameters. ACM Trans. Knowl. Discov. from Data, 1(1):1–40, 2007.