A Song of Ice and Fire
This is the fictional social network of the series of fantasy novels "A Song of
Ice and Fire" by George R. R. Martin (1996–present). An edge denotes that
two characters are mentioned within fifteen words of each other; edge
multiplicities denote the number of such appearances. This version of the
dataset covers books one to five.
Metadata
Statistics
| Size | n = | 796
|
| Volume | m = | 32,629
|
| Unique edge count | m̿ = | 2,823
|
| Loop count | l = | 0
|
| Wedge count | s = | 81,158
|
| Claw count | z = | 1,766,472
|
| Cross count | x = | 37,318,726
|
| Triangle count | t = | 5,655
|
| Square count | q = | 78,782
|
| 4-Tour count | T4 = | 960,534
|
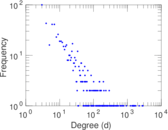
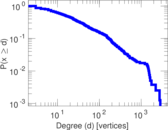
| Maximum degree | dmax = | 122
|
| Average degree | d = | 81.982 4
|
| Fill | p = | 0.008 921 97
|
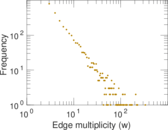
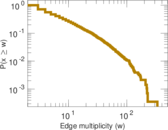
| Average edge multiplicity | m̃ = | 11.558 3
|
| Size of LCC | N = | 796
|
| Diameter | δ = | 9
|
| 50-Percentile effective diameter | δ0.5 = | 2.848 72
|
| 90-Percentile effective diameter | δ0.9 = | 4.143 66
|
| Median distance | δM = | 3
|
| Mean distance | δm = | 3.410 82
|
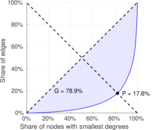
| Gini coefficient | G = | 0.788 981
|
| Balanced inequality ratio | P = | 0.176 331
|
| Relative edge distribution entropy | Her = | 0.886 437
|
| Power law exponent | γ = | 1.779 17
|
| Tail power law exponent | γt = | 2.321 00
|
| Tail power law exponent with p | γ3 = | 2.321 00
|
| p-value | p = | 0.051 000 0
|
| Degree assortativity | ρ = | −0.115 391
|
| Degree assortativity p-value | pρ = | 3.389 13 × 10−18
|
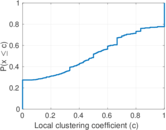
| Clustering coefficient | c = | 0.209 037
|
| Spectral norm | α = | 953.787
|
| Algebraic connectivity | a = | 0.752 030
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.717 35
|
| Non-bipartivity | bA = | 0.578 642
|
| Normalized non-bipartivity | bN = | 0.123 682
|
| Algebraic non-bipartivity | χ = | 0.203 828
|
| Spectral bipartite frustration | bK = | 0.007 184 18
|
| Controllability | C = | 168
|
| Relative controllability | Cr = | 0.211 055
|
Plots
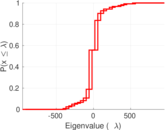
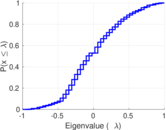

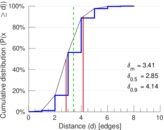
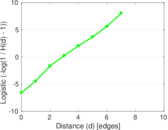
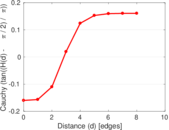
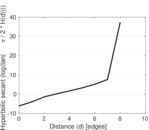
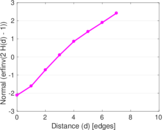
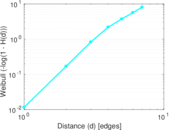
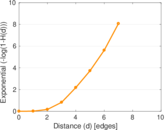


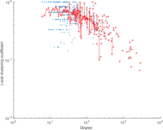

Matrix decompositions plots
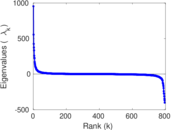
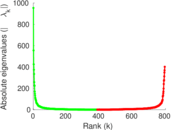
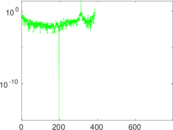
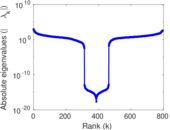
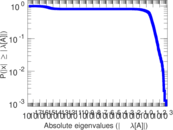
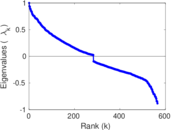
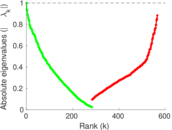
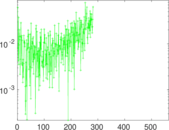
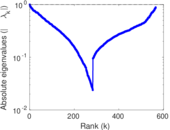
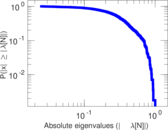
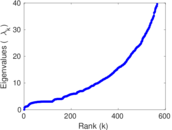
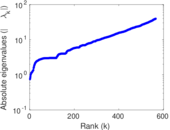
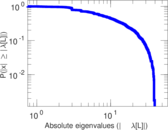
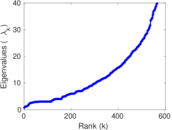
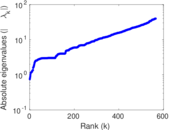
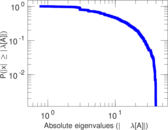
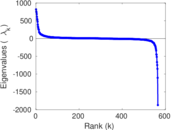
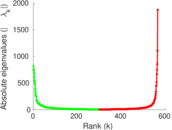
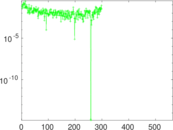
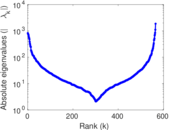
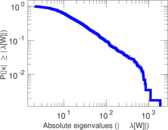
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee



















































