arXiv astro-ph

This is the collaboration graph of authors of scientific papers from the arXiv's Astrophysics (astro-ph) section. An edge between two authors represents a common publication.

Metadata

CodeAP
Internal nameca-AstroPh
NamearXiv astro-ph
Data sourcehttp://snap.stanford.edu/data/ca-AstroPh.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Co-authorship network
Node meaningAuthor
Edge meaningCollaboration
Network formatUnipartite, undirected
Edge typeUnweighted, no multiple edges
LoopsDoes not contain loops
Join Is the join of an underlying network

Statistics

Size n =18,771
Volume m =198,050
Loop count l =0
Wedge count s =12,749,380
Claw count z =545,677,552
Cross count x =28,436,651,241
Triangle count t =1,351,441
Square count q =44,916,549
4-Tour count T4 =410,726,012
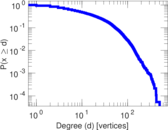
Maximum degree dmax =504
Average degree d =21.101 7
Fill p =0.001 124 22
Size of LCC N =17,903
Diameter δ =14
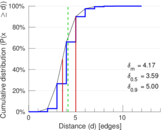
50-Percentile effective diameter δ0.5 =3.593 59
90-Percentile effective diameter δ0.9 =5.002 79
Median distance δM =4
Mean distance δm =4.174 33
Gini coefficient G =0.610 511
Balanced inequality ratio P =0.265 125
Relative edge distribution entropy Her =0.931 468
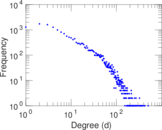
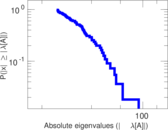
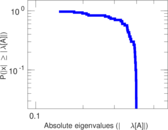
Power law exponent γ =1.439 22
Tail power law exponent γt =2.861 00
Tail power law exponent with p γ3 =2.861 00
p-value p =0.000 00
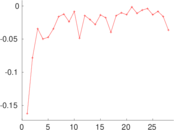
Degree assortativity ρ =+0.205 129
Degree assortativity p-value pρ =0.000 00
Clustering coefficient c =0.318 002
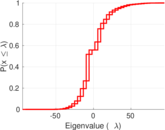
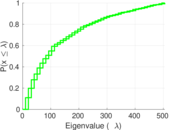
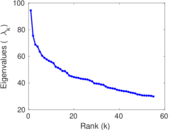
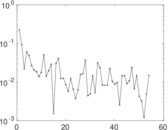
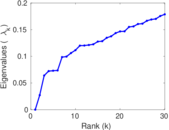
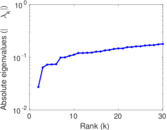
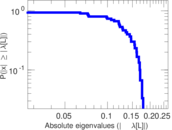
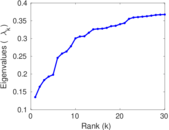
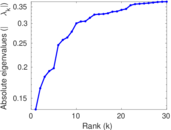
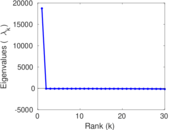
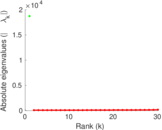
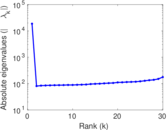
Spectral norm α =94.429 6
Algebraic connectivity a =0.027 215 7
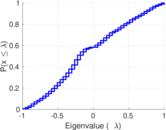
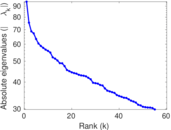
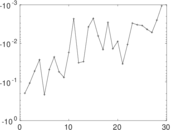
Spectral separation |λ1[A] / λ2[A]| =1.251 04
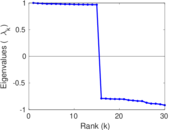
Non-bipartivity bA =0.700 817
Normalized non-bipartivity bN =0.084 055 4
Algebraic non-bipartivity χ =0.135 163
Spectral bipartite frustration bK =0.001 535 64
Controllability C =538
Relative controllability Cr =0.028 661 2

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

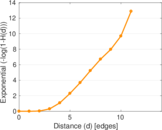
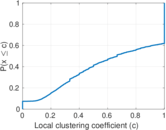
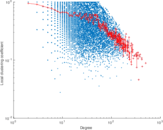
Matrix decompositions plots

Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Jure Leskovec, Jon Kleinberg, and Christos Faloutsos. Graph evolution: Densification and shrinking diameters. ACM Trans. Knowl. Discov. from Data, 1(1):1–40, 2007.