arXiv hep-th
This is the network of publications in the arXiv's High Energy Physics –
Theory (hep-th) section. The directed links that connect the publications are
citations.
Metadata
Statistics
| Size | n = | 27,770
|
| Volume | m = | 352,807
|
| Loop count | l = | 39
|
| Wedge count | s = | 37,101,609
|
| Claw count | z = | 8,172,939,577
|
| Cross count | x = | 3,139,197,249,029
|
| Triangle count | t = | 1,478,735
|
| Square count | q = | 63,698,507
|
| 4-Tour count | T4 = | 658,699,062
|
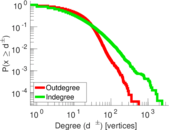
| Maximum degree | dmax = | 2,468
|
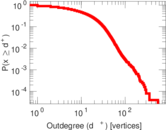
| Maximum outdegree | d+max = | 562
|
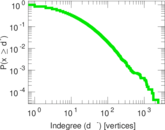
| Maximum indegree | d−max = | 2,414
|
| Average degree | d = | 25.409 2
|
| Fill | p = | 0.000 457 494
|
| Size of LCC | N = | 27,400
|
| Size of LSCC | Ns = | 7,464
|
| Relative size of LSCC | Nrs = | 0.268 779
|
| Diameter | δ = | 15
|
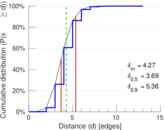
| 50-Percentile effective diameter | δ0.5 = | 3.689 70
|
| 90-Percentile effective diameter | δ0.9 = | 5.355 75
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 4.269 57
|
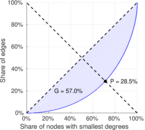
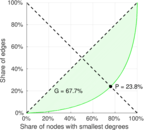
| Gini coefficient | G = | 0.570 239
|
| Balanced inequality ratio | P = | 0.285 445
|
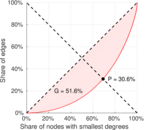
| Outdegree balanced inequality ratio | P+ = | 0.306 250
|
| Indegree balanced inequality ratio | P− = | 0.238 017
|
| Relative edge distribution entropy | Her = | 0.937 827
|
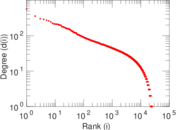
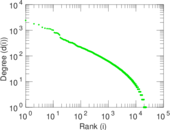
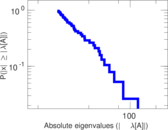
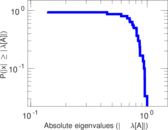
| Power law exponent | γ = | 1.389 89
|
| Tail power law exponent | γt = | 3.111 00
|
| Tail power law exponent with p | γ3 = | 3.111 00
|
| p-value | p = | 0.002 000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 4.131 00
|
| Outdegree p-value | po = | 0.140 000
|
| Indegree tail power law exponent with p | γ3,i = | 2.691 00
|
| Indegree p-value | pi = | 0.033 000 0
|
| Degree assortativity | ρ = | −0.030 312 5
|
| Degree assortativity p-value | pρ = | 7.117 76 × 10−143
|
| In/outdegree correlation | ρ± = | +0.277 949
|
| Clustering coefficient | c = | 0.119 569
|
| Directed clustering coefficient | c± = | 0.199 169
|
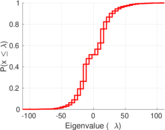
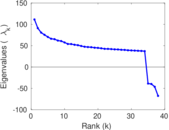
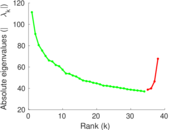
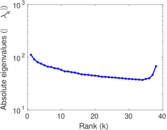
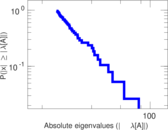
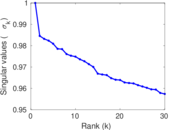
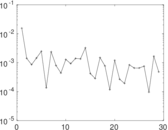
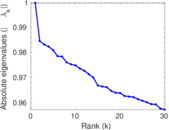
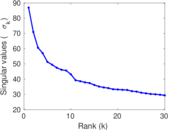
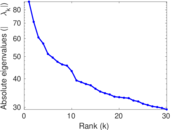
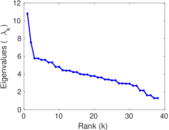
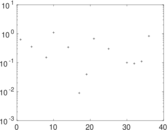
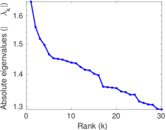
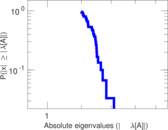
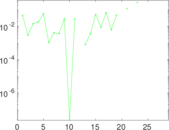
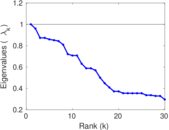
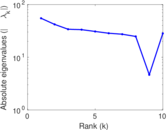
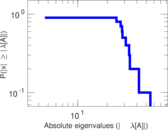
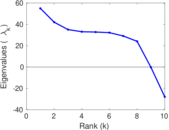
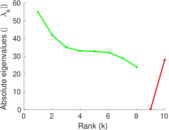
| Spectral norm | α = | 111.322
|
| Operator 2-norm | ν = | 85.160 7
|
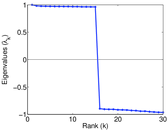
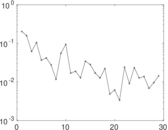
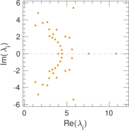
| Cyclic eigenvalue | π = | 10.801 1
|
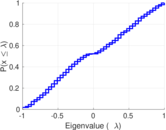
| Algebraic connectivity | a = | 0.064 997 8
|
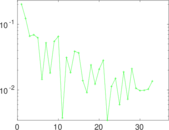
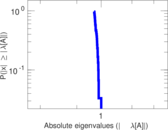
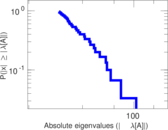
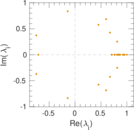
| Spectral separation | |λ1[A] / λ2[A]| = | 1.223 53
|
| Reciprocity | y = | 0.002 848 58
|
| Non-bipartivity | bA = | 0.391 840
|
| Normalized non-bipartivity | bN = | 0.036 274 2
|
| Algebraic non-bipartivity | χ = | 0.065 072 3
|
| Spectral bipartite frustration | bK = | 0.000 633 054
|
| Controllability | C = | 6,718
|
| Relative controllability | Cr = | 0.241 916
|
Plots

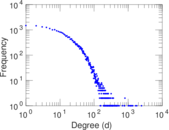
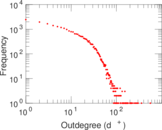
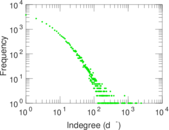
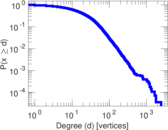
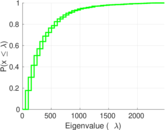
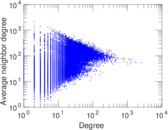
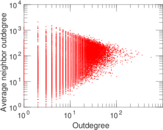
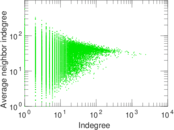
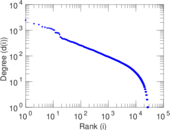
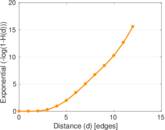



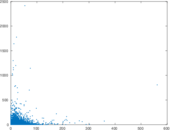
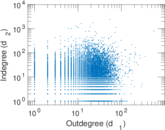
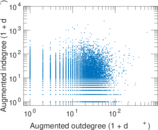
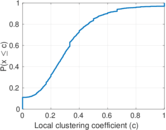
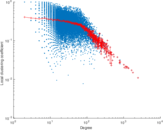

Matrix decompositions plots
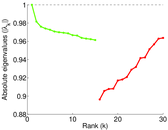
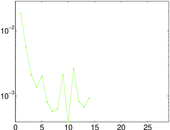
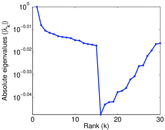
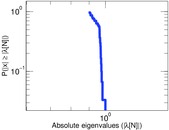
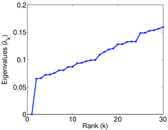
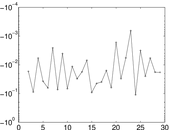
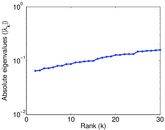
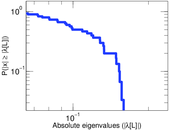
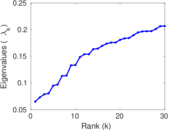
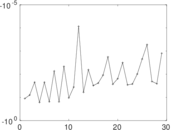
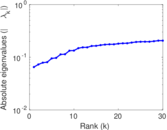
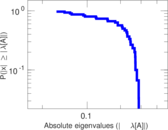
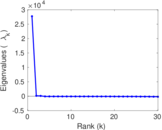
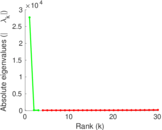
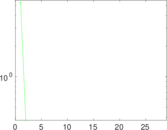
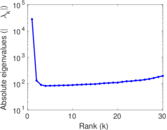
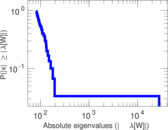
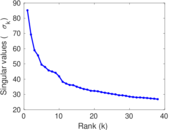
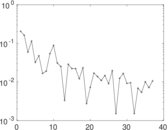
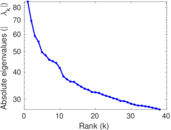
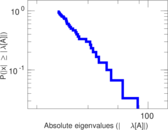
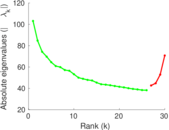
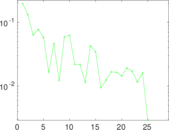
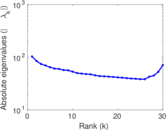
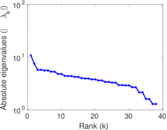
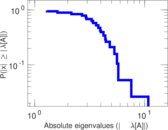
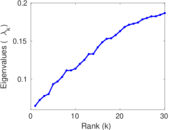
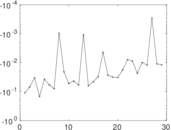
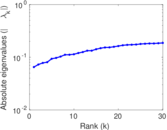
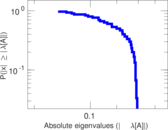
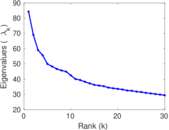
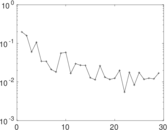
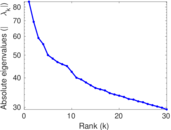
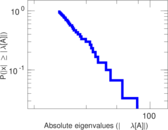
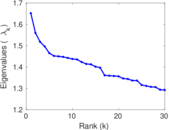
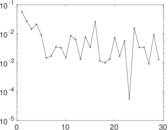
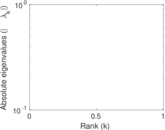
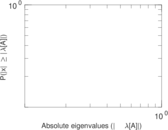
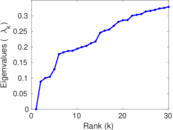
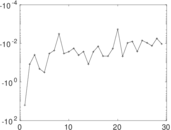
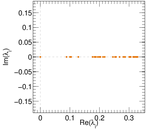
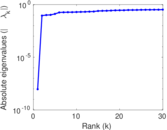
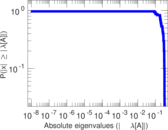
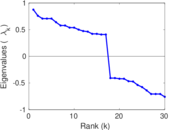
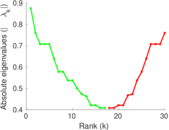
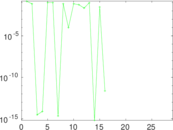
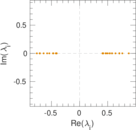
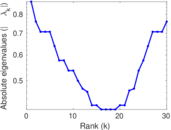
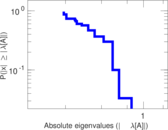
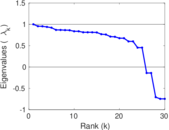
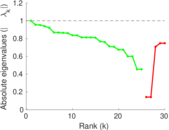

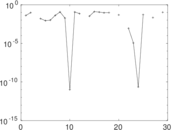
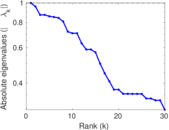
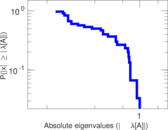
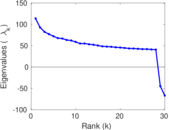
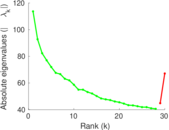
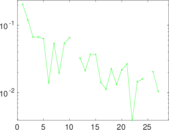
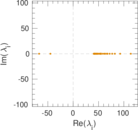
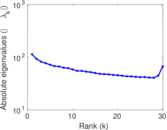
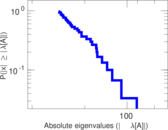
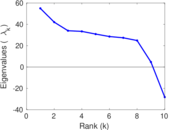
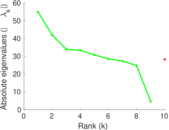
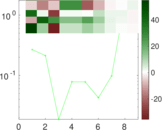
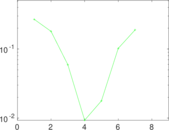
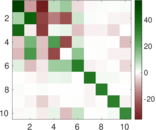
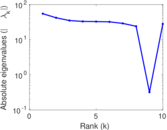
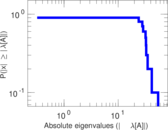
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Jure Leskovec, Jon Kleinberg, and Christos Faloutsos.
Graph evolution: Densification and shrinking diameters.
ACM Trans. Knowl. Discov. from Data, 1(1):1–40, 2007.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee









































































































































