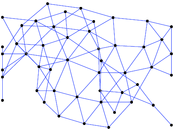
Contiguous USA

These are the 48 contiguous states and the District of Columbia of the United States of America (the USA). They include all states except the states of Alaska and Hawaii, which are not connected by land with the other states, and include the District of Columbia (DC). An edge denotes that two states share a border. The US states in the configuration given by this dataset exist since February 14, 1912, when Arizona was admitted as the 48th state, and is current as of 2014. The states of Alaska and Hawaii were admitted as the 49th and 50th states in 1959, but are not contiguous with the other states, and are not reflected in this dataset.

Metadata

CodeCU
Internal namecontiguous-usa
NameContiguous USA
Data sourcehttp://www-cs-faculty.stanford.edu/~uno/sgb.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Infrastructure network
Dataset timestamp 1912
Node meaningState
Edge meaningBorder
Network formatUnipartite, undirected
Edge typeUnweighted, no multiple edges
LoopsDoes not contain loops

Statistics

Size n =49
Volume m =107
Loop count l =0
Wedge count s =421
Claw count z =494
Cross count x =382
Triangle count t =57
Square count q =70
4-Tour count T4 =2,458
Maximum degree dmax =8
Average degree d =4.367 35
Fill p =0.090 986 4
Size of LCC N =49
Diameter δ =11
50-Percentile effective diameter δ0.5 =3.476 64
90-Percentile effective diameter δ0.9 =6.983 76
Median distance δM =4
Mean distance δm =4.255 02
Gini coefficient G =0.201 221
Balanced inequality ratio P =0.425 234
Relative edge distribution entropy Her =0.982 602
Power law exponent γ =1.715 37
Tail power law exponent γt =8.991 00
Tail power law exponent with p γ3 =8.991 00
p-value p =0.668 000
Degree assortativity ρ =+0.233 397
Degree assortativity p-value pρ =0.000 577 516
Clustering coefficient c =0.406 176
Spectral norm α =5.318 55
Algebraic connectivity a =0.098 048 7
Spectral separation |λ1[A] / λ2[A]| =1.166 23
Non-bipartivity bA =0.456 938
Normalized non-bipartivity bN =0.281 820
Algebraic non-bipartivity χ =0.483 588
Spectral bipartite frustration bK =0.027 682 0
Controllability C =3
Relative controllability Cr =0.061 224 5

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

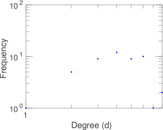
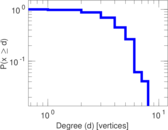
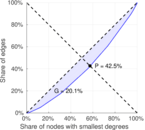
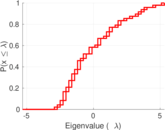
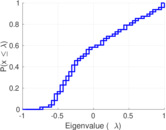
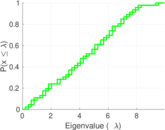
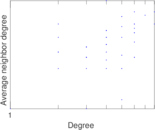
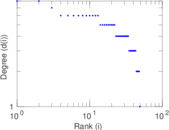
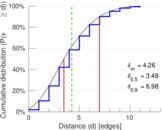
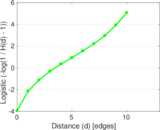
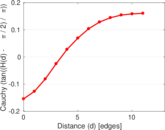
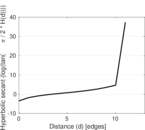
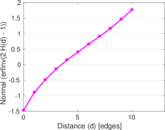
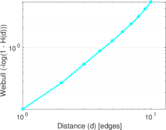
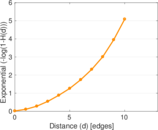
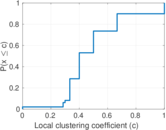
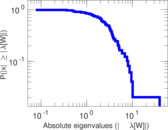
Matrix decompositions plots

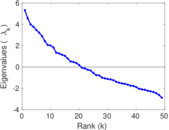
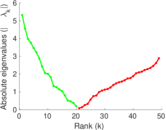
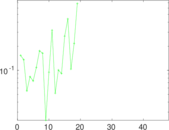
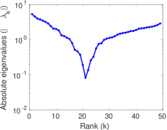
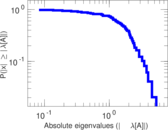
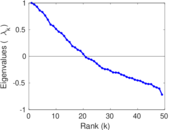
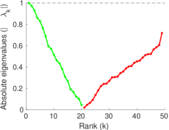
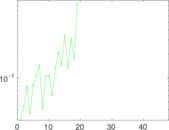
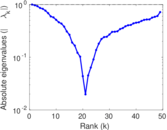
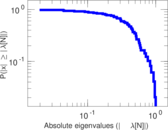
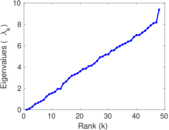
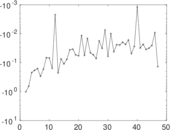
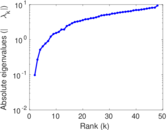
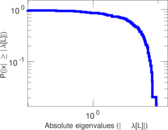
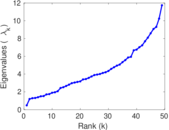
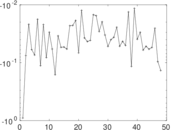
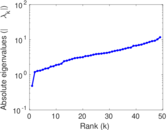
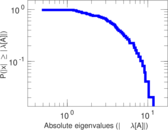
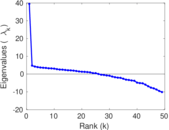
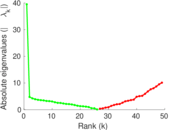
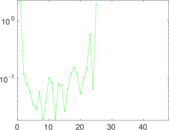
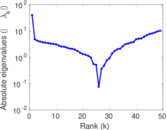
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Donald E. Knuth. The Art of Computer Programming, Volume 4, Fascicle 0: Introduction to Combinatorial and Boolean Functions. Addison-Wesley, 2008.