Writers
This is the bipartite writer network of DBpedia. Nodes are writers (persons)
and their works. The edges correspond to the
<http://dbpedia.org/ontology/writer> relationships in DBpedia.
Metadata
Statistics
| Size | n = | 135,569
|
| Left size | n1 = | 89,356
|
| Right size | n2 = | 46,213
|
| Volume | m = | 144,340
|
| Wedge count | s = | 1,125,315
|
| Claw count | z = | 20,262,025
|
| Cross count | x = | 625,244,181
|
| Square count | q = | 126,753
|
| 4-Tour count | T4 = | 5,804,216
|
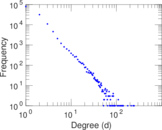
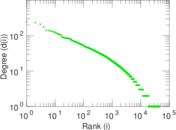
| Maximum degree | dmax = | 246
|
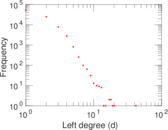
| Maximum left degree | d1max = | 42
|
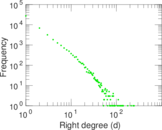
| Maximum right degree | d2max = | 246
|
| Average degree | d = | 2.129 40
|
| Average left degree | d1 = | 1.615 34
|
| Average right degree | d2 = | 3.123 36
|
| Fill | p = | 3.495 42 × 10−5
|
| Size of LCC | N = | 74,761
|
| Diameter | δ = | 60
|
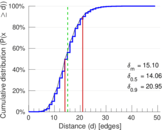
| 50-Percentile effective diameter | δ0.5 = | 14.057 3
|
| 90-Percentile effective diameter | δ0.9 = | 20.951 0
|
| Median distance | δM = | 15
|
| Mean distance | δm = | 15.102 1
|
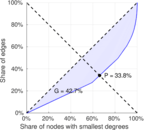
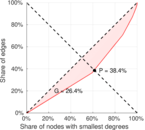
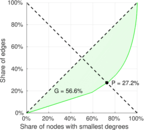
| Gini coefficient | G = | 0.451 333
|
| Balanced inequality ratio | P = | 0.338 039
|
| Left balanced inequality ratio | P1 = | 0.383 941
|
| Right balanced inequality ratio | P2 = | 0.271 893
|
| Relative edge distribution entropy | Her = | 0.958 118
|
| Power law exponent | γ = | 3.313 17
|
| Tail power law exponent | γt = | 2.721 00
|
| Tail power law exponent with p | γ3 = | 2.721 00
|
| p-value | p = | 0.000 00
|
| Left tail power law exponent with p | γ3,1 = | 5.611 00
|
| Left p-value | p1 = | 0.042 000 0
|
| Right tail power law exponent with p | γ3,2 = | 1.991 00
|
| Right p-value | p2 = | 0.000 00
|
| Degree assortativity | ρ = | −0.026 571 9
|
| Degree assortativity p-value | pρ = | 5.701 04 × 10−24
|
| Spectral norm | α = | 16.608 7
|
| Algebraic connectivity | a = | 0.000 546 041
|
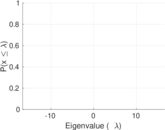
| Spectral separation | |λ1[A] / λ2[A]| = | 1.048 92
|
| Controllability | C = | 55,409
|
| Relative controllability | Cr = | 0.408 717
|
Plots

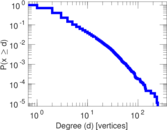
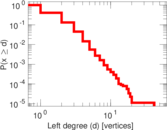
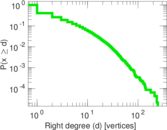
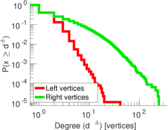
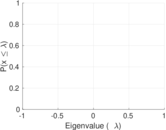
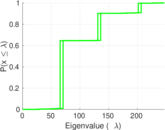


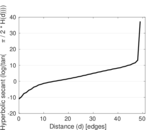
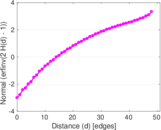
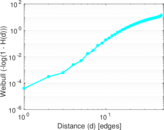
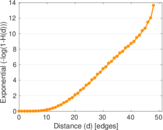




Matrix decompositions plots
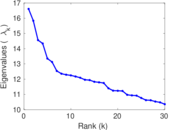
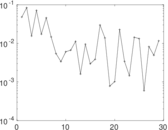
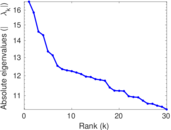
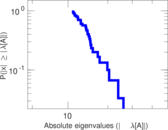
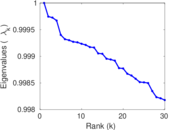
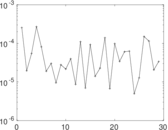
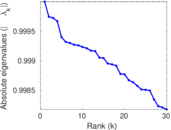
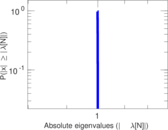
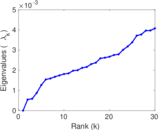
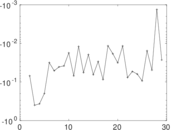
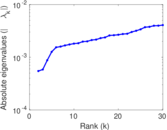
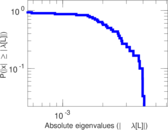
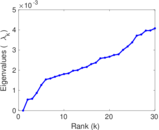
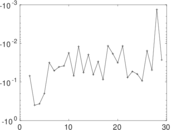
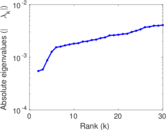
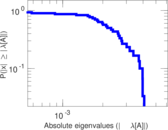
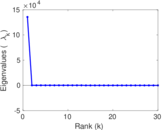
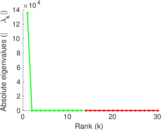
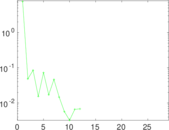
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Sören Auer, Christian Bizer, Georgi Kobilarov, Jens Lehmann, Richard Cyganiak,
and Zachary Ives.
DBpedia: A nucleus for a web of open data.
In Proc. Int. Semant. Web Conf., pages 722–735, 2008.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee