Caenorhabditis elegans (metabolic)

This is the metabolic network of Caenorhabditis elegans. We acquired the network from the DIMACS10 project, which acquired it from Alex Arena's website, which took it from the article by Jeong et al., which is based on data from the WIT database. To cite the paper by Jeong and colleagues, which analyses 43 such networks: "This integrated pathway–genome database predicts the existence of a given metabolic pathway on the basis of the annotated genome of an organism combined with firmly established data from the biochemical literature. As 18 of the 43 genomes deposited in the database are not yet fully sequenced, and a substantial portion of the identified open reading frames are functionally unassigned, the list of enzymes, and consequently the list of substrates and reactions, will certainly be expanded in the future. Nevertheless, this publicly available database represents our best approximation for the metabolic pathways in 43 organisms and provides sufficient data for their unambiguous statistical analysis. [...] We first established a graph theoretic representation of the biochemical reactions taking place in a given metabolic network. In this representation, a metabolic network is built up of nodes, the substrates, that are connected to one another through links, which are the actual metabolic reactions. The physical entity of the link is the temporary educt–educt complex itself, in which enzymes provide the catalytic scaffolds for the reactions yielding products, which in turn can become educts for subsequent reactions."

Metadata

CodeCE
Internal namedimacs10-celegans_metabolic
NameCaenorhabditis elegans (metabolic)
Data sourcehttps://www.cc.gatech.edu/dimacs10/archive/clustering.shtml
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Metabolic network
Node meaningSubstrate
Edge meaningMetabolic reaction
Network formatUnipartite, undirected
Edge typeUnweighted, no multiple edges
LoopsDoes not contain loops
Snapshot Is a snapshot and likely to not contain all data

Statistics

Size n =453
Volume m =2,025
Loop count l =0
Wedge count s =79,173
Claw count z =3,352,172
Cross count x =153,983,040
Triangle count t =3,284
Square count q =50,289
4-Tour count T4 =723,054
Maximum degree dmax =237
Average degree d =8.940 40
Fill p =0.019 779 6
Size of LCC N =453
Diameter δ =7
50-Percentile effective diameter δ0.5 =2.143 50
90-Percentile effective diameter δ0.9 =3.169 35
Median distance δM =3
Mean distance δm =2.676 27
Gini coefficient G =0.494 803
Balanced inequality ratio P =0.321 481
Relative edge distribution entropy Her =0.898 264
Power law exponent γ =1.565 69
Tail power law exponent γt =2.631 00
Tail power law exponent with p γ3 =2.631 00
p-value p =0.050 000 0
Degree assortativity ρ =−0.225 821
Degree assortativity p-value pρ =5.419 17 × 10−48
Clustering coefficient c =0.124 436
Spectral norm α =26.308 5
Algebraic connectivity a =0.258 000
Spectral separation |λ1[A] / λ2[A]| =1.752 33
Non-bipartivity bA =0.429 332
Normalized non-bipartivity bN =0.200 551
Algebraic non-bipartivity χ =0.293 557
Spectral bipartite frustration bK =0.008 208 72
Controllability C =7
Relative controllability Cr =0.015 452 5

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

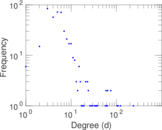
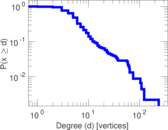
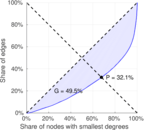
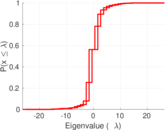
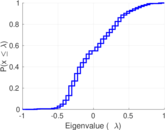
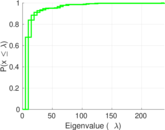
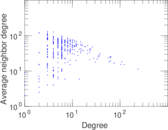
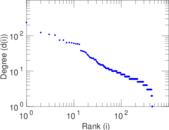
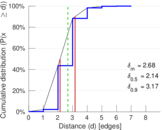
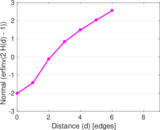
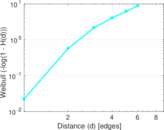
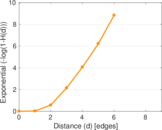
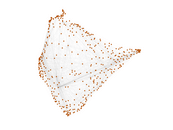
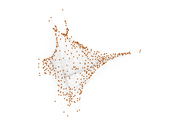
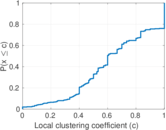
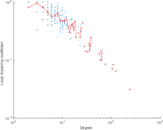
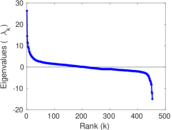
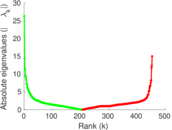
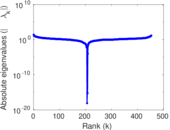
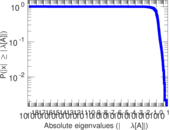
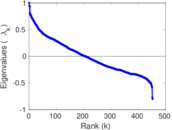
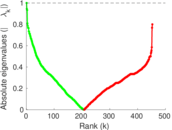
Matrix decompositions plots

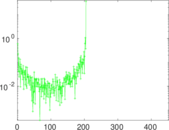
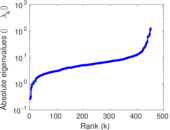
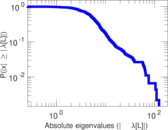
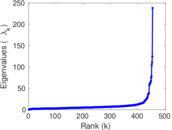
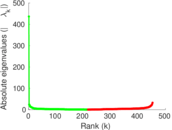
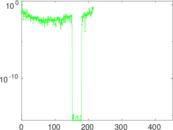
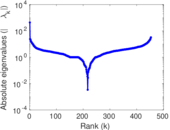
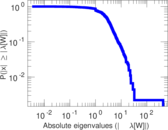
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Jordi Duch and Alex Arenas. Community detection in complex networks using extremal optimization. Phys. Rev. E, 72(2):027104, 2005.
[3] Hawoong Jeong, Bálint Tombor, Réka Albert, Zoltan N. Oltvai, and Albert-László Barabási. The large-scale organization of metabolic networks. Nature, 407:651–654, 2000.
[4] Ross Overbeek, Niels Larsen, Gordon D. Pusch, Mark D'Souza, Evgeni Selkov Jr., Nikos Kyrpides, Michael Fonstein, Natalia Maltsev, and Evgeni Selkov. WIT: Integrated system for high-throughput genome sequence analysis and metabolic reconstruction. Nucleic Acids Res., 28(1):123–125, 2000.