Caenorhabditis elegans (neural)
This is a weighted directed network representing the neural network of
Caenorhabditis elegans. The original network had directed edges
allowing multiple parallel edges with integer weights. In this version, the
network is undirected, allows no multiple edges, and the given edge weights are
the sum of the original edge weights. As described in the original publication
by J. G. White and colleagues, the data was assembled by hand and may contain a
small number of errors. To cite: "We are reasonably confident that the
structure that we present is substantially correct and gives a reasonable
picture of the organization of the nervous system in a typical C.
elegans hermaphrodite."
Metadata
Statistics
| Size | n = | 297
|
| Volume | m = | 4,296
|
| Loop count | l = | 0
|
| Wedge count | s = | 53,804
|
| Claw count | z = | 7,341,160
|
| Cross count | x = | 307,724,064
|
| Triangle count | t = | 3,241
|
| Square count | q = | 44,636
|
| 4-Tour count | T4 = | 576,600
|
| Maximum degree | dmax = | 268
|
| Maximum outdegree | d+max = | 134
|
| Maximum indegree | d−max = | 134
|
| Average degree | d = | 28.929 3
|
| Fill | p = | 0.048 867 0
|
| Size of LCC | N = | 297
|
| Size of LSCC | Ns = | 297
|
| Relative size of LSCC | Nrs = | 1.000 00
|
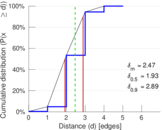
| Diameter | δ = | 5
|
| 50-Percentile effective diameter | δ0.5 = | 1.929 02
|
| 90-Percentile effective diameter | δ0.9 = | 2.891 73
|
| Median distance | δM = | 2
|
| Mean distance | δm = | 2.469 83
|
| Gini coefficient | G = | 0.385 480
|
| Balanced inequality ratio | P = | 0.362 430
|
| Outdegree balanced inequality ratio | P+ = | 0.362 430
|
| Indegree balanced inequality ratio | P− = | 0.362 430
|
| Relative edge distribution entropy | Her = | 0.950 953
|
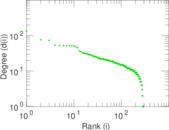
| Power law exponent | γ = | 1.421 43
|
| Tail power law exponent | γt = | 3.341 00
|
| Tail power law exponent with p | γ3 = | 3.341 00
|
| p-value | p = | 0.658 000
|
| Outdegree tail power law exponent with p | γ3,o = | 3.341 00
|
| Outdegree p-value | po = | 0.661 000
|
| Indegree tail power law exponent with p | γ3,i = | 3.341 00
|
| Indegree p-value | pi = | 0.649 000
|
| Degree assortativity | ρ = | −0.163 199
|
| Degree assortativity p-value | pρ = | 4.990 05 × 10−27
|
| In/outdegree correlation | ρ± = | +1.000 00
|
| Clustering coefficient | c = | 0.180 711
|
| Directed clustering coefficient | c± = | 0.180 711
|
| Spectral norm | α = | 412.892
|
| Operator 2-norm | ν = | 206.446
|
| Cyclic eigenvalue | π = | 206.446
|
| Algebraic connectivity | a = | 1.883 17
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.234 66
|
| Reciprocity | y = | 1.000 00
|
| Non-bipartivity | bA = | 0.473 226
|
| Normalized non-bipartivity | bN = | 0.451 282
|
| Algebraic non-bipartivity | χ = | 0.843 939
|
| Spectral bipartite frustration | bK = | 0.014 586 2
|
| Controllability | C = | 15
|
| Relative controllability | Cr = | 0.050 505 1
|
Plots
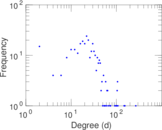
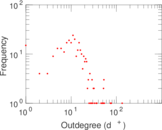
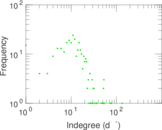
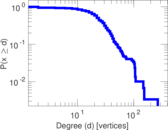
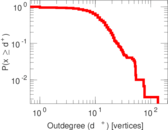
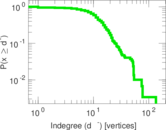
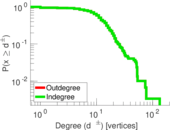
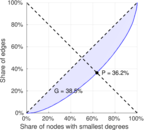
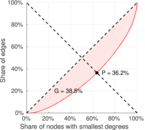
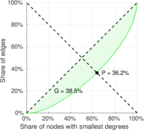
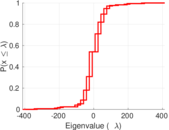
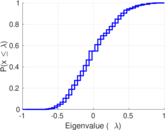
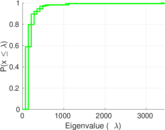



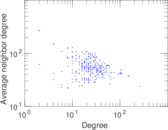


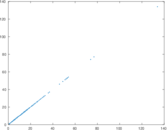
Matrix decompositions plots
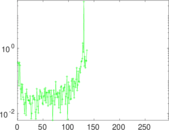
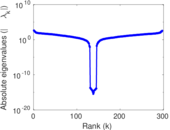
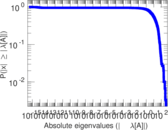
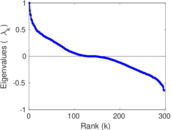
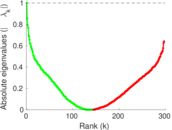
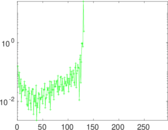
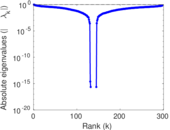
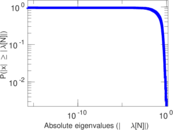
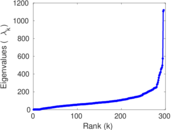
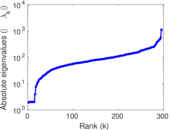
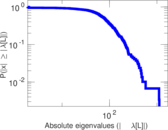
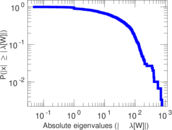
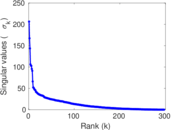
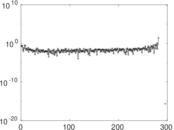
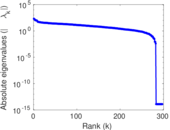
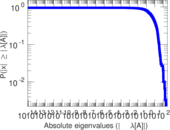
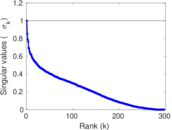
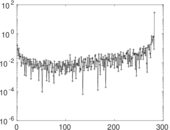
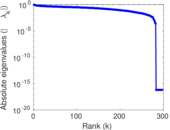
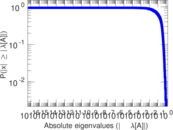
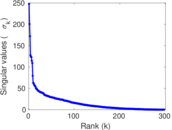
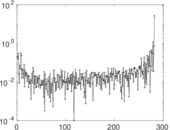
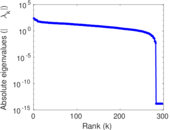
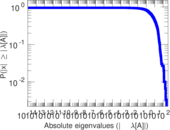
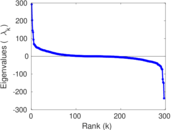
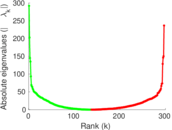
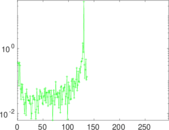
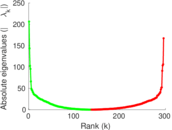
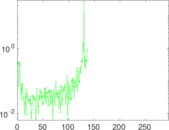
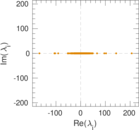
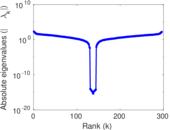
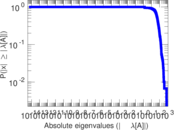
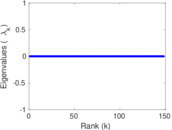
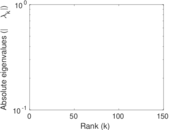
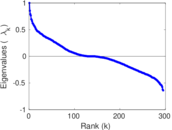
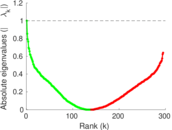
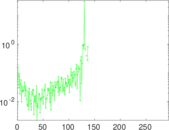
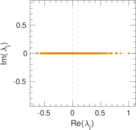
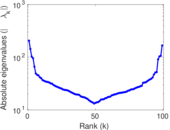
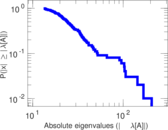
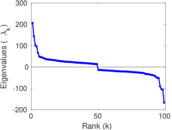
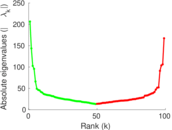
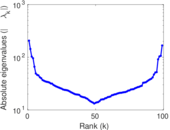
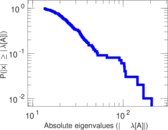
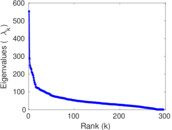
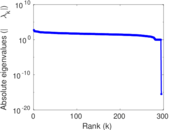
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Duncan J. Watts and Steven H. Strogatz.
Collective dynamics of `small-world' networks.
Nature, 393(1):440–442, 1998.
|
|
[3]
|
John G. White, E. Southgate, J. N. Thomson, and S. Brenner.
The structure of the nervous system of the nematode Caenorhabditis
elegans.
Phil. Trans. R. Soc. Lond, 314:1–340, 1986.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee