Condensed matter (2003)

These are scientific collaboration in the area of Condensed Matter (physics). It contains co-authorships from papers uploaded to arXiv in the "condensed matter" section, in the time range 1995 to 2003.

Metadata

CodeCM
Internal namedimacs10-cond-mat-2003
NameCondensed matter (2003)
Data sourcehttps://www.cc.gatech.edu/dimacs10/archive/clustering.shtml
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Co-authorship network
Dataset timestamp 1995-01-01 ⋯ 2003-06-30
Node meaningAuthor
Edge meaningCo-authorship
Network formatUnipartite, undirected
Edge typeUnweighted, no multiple edges
LoopsDoes not contain loops
Join Is the join of an underlying network
Multiplicity Does not have multiple edges, but the underlying data has

Statistics

Size n =30,460
Volume m =120,029
Loop count l =0
Wedge count s =2,489,239
Claw count z =42,828,081
Cross count x =976,339,458
Triangle count t =232,994
Square count q =2,200,663
4-Tour count T4 =27,802,318
Maximum degree dmax =202
Average degree d =7.881 09
Fill p =0.000 258 744
Size of LCC N =27,519
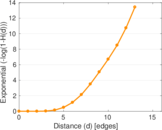
Diameter δ =16
50-Percentile effective diameter δ0.5 =5.372 28
90-Percentile effective diameter δ0.9 =7.195 30
Median distance δM =6
Mean distance δm =5.911 84
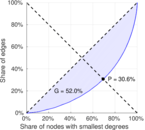
Gini coefficient G =0.519 927
Balanced inequality ratio P =0.305 909
Relative edge distribution entropy Her =0.950 974
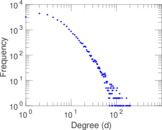
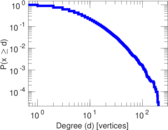
Power law exponent γ =1.631 95
Tail power law exponent γt =3.621 00
Tail power law exponent with p γ3 =3.621 00
p-value p =0.061 000 0
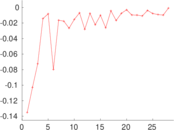
Degree assortativity ρ =+0.178 214
Degree assortativity p-value pρ =0.000 00
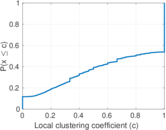
Clustering coefficient c =0.280 801
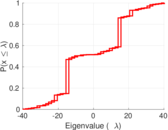
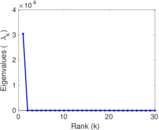
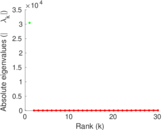
Spectral norm α =40.309 7
Algebraic connectivity a =0.027 584 2
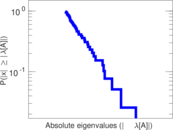
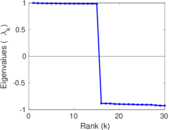
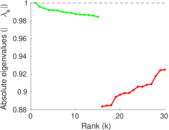
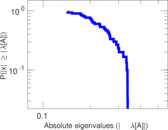
Spectral separation |λ1[A] / λ2[A]| =1.177 90
Non-bipartivity bA =0.607 353
Normalized non-bipartivity bN =0.075 005 1
Algebraic non-bipartivity χ =0.128 075
Spectral bipartite frustration bK =0.003 792 04
Controllability C =2,026
Relative controllability Cr =0.066 513 5

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

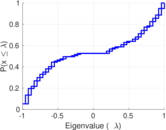
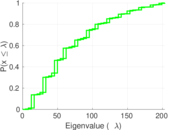
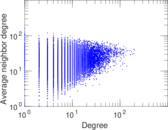
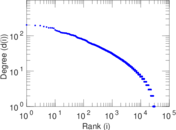
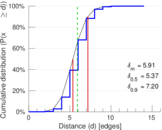
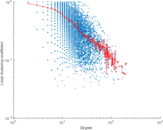
Matrix decompositions plots

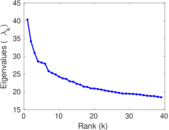
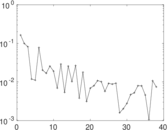
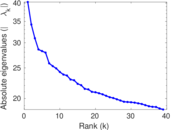
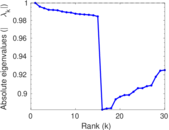
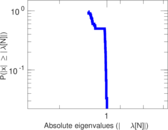
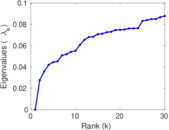
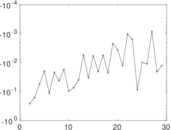
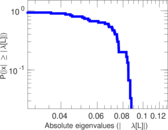
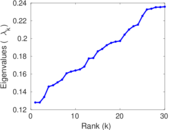
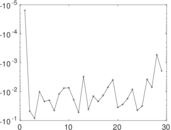
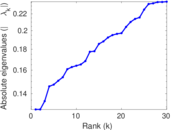
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Mark E. J. Newman. The structure of scientific collaboration networks. Proc. Natl. Acad. Sci. U.S.A., 98(2):404–409, 2001.
[3] Jordi Duch and Alex Arenas. Community detection in complex networks using extremal optimization. Phys. Rev. E, 72(2):027104, 2005.