 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee
This is "[a] network of books about US politics published around the time of the 2004 presidential election and sold by the online bookseller Amazon.com. Edges between books represent frequent copurchasing of books by the same buyers. The network was compiled by V. Krebs and is unpublished, but can found on Krebs' web site (http://www.orgnet.com/). Thanks to Valdis Krebs for permission to post these data on this web site."
| Code | PB
| |
| Internal name | dimacs10-polbooks
| |
| Name | Political books | |
| Data source | https://www.cc.gatech.edu/dimacs10/archive/clustering.shtml | |
| Availability | Dataset is available for download | |
| Consistency check | Dataset passed all tests | |
| Category | Miscellaneous network | |
| Dataset timestamp | 2004 | |
| Node meaning | Book | |
| Edge meaning | Co-purchase | |
| Network format | Unipartite, undirected | |
| Edge type | Unweighted, no multiple edges | |
| Loops | Does not contain loops | |
| Snapshot | Is a snapshot and likely to not contain all data | |
| Join | Is the join of an underlying network | |
| Multiplicity | Does not have multiple edges, but the underlying data has | |
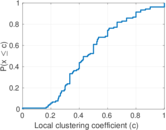
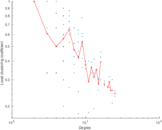
| k-Core | Only nodes with degree larger than a given threshold are included |

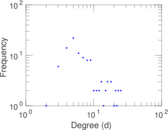
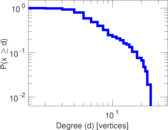
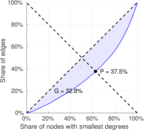
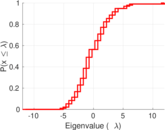
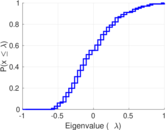
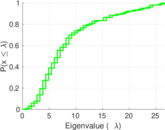


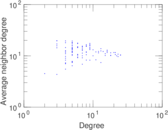
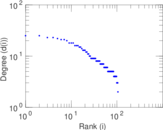
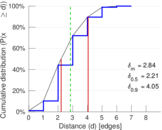
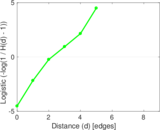
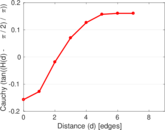



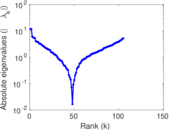
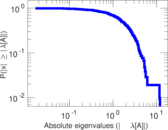
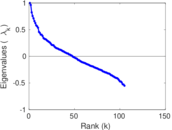
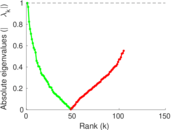
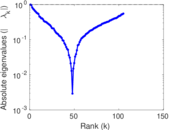
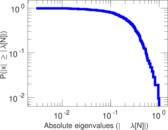
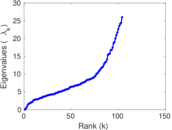
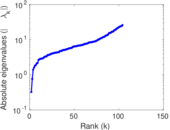
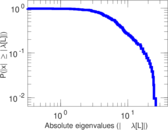
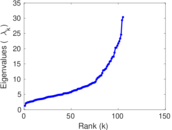
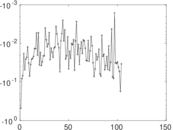
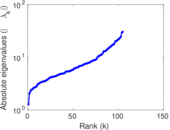
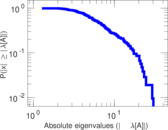
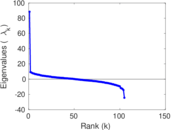
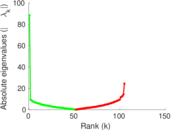
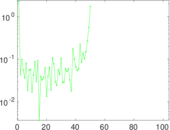
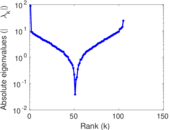
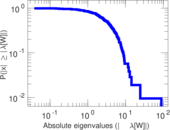
| [1] | Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ] |