Douban
This is the social network of Douban, a Chinese online recommendation site.
The network is undirected and unweighted.
Metadata
Statistics
| Size | n = | 154,908
|
| Volume | m = | 327,162
|
| Loop count | l = | 0
|
| Wedge count | s = | 11,745,116
|
| Claw count | z = | 269,719,710
|
| Cross count | x = | 6,564,312,495
|
| Triangle count | t = | 40,612
|
| Square count | q = | 750,163
|
| 4-Tour count | T4 = | 53,636,092
|
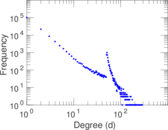
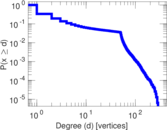
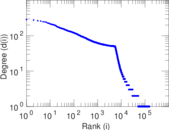
| Maximum degree | dmax = | 287
|
| Average degree | d = | 4.223 95
|
| Fill | p = | 2.726 77 × 10−5
|
| Size of LCC | N = | 154,908
|
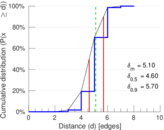
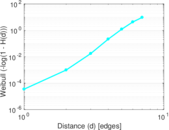
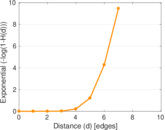
| Diameter | δ = | 9
|
| 50-Percentile effective diameter | δ0.5 = | 4.602 48
|
| 90-Percentile effective diameter | δ0.9 = | 5.695 94
|
| Median distance | δM = | 5
|
| Mean distance | δm = | 5.100 46
|
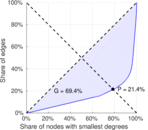
| Gini coefficient | G = | 0.694 496
|
| Balanced inequality ratio | P = | 0.214 079
|
| Relative edge distribution entropy | Her = | 0.889 699
|
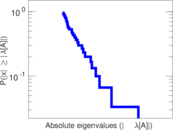
| Power law exponent | γ = | 2.970 61
|
| Tail power law exponent | γt = | 2.081 00
|
| Tail power law exponent with p | γ3 = | 2.081 00
|
| p-value | p = | 0.000 00
|
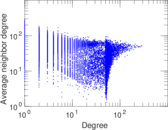
| Degree assortativity | ρ = | −0.180 331
|
| Degree assortativity p-value | pρ = | 0.000 00
|
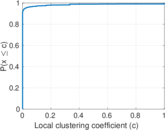
| Clustering coefficient | c = | 0.010 373 3
|
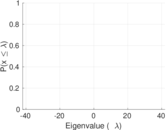
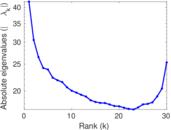
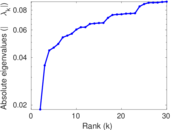
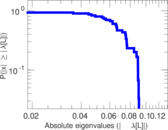
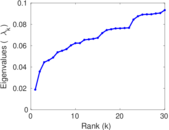
| Spectral norm | α = | 41.968 2
|
| Algebraic connectivity | a = | 0.018 767 2
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.373 38
|
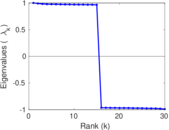
| Non-bipartivity | bA = | 0.395 394
|
| Normalized non-bipartivity | bN = | 0.009 618 19
|
| Algebraic non-bipartivity | χ = | 0.018 791 7
|
| Spectral bipartite frustration | bK = | 0.001 112 21
|
| Controllability | C = | 137,540
|
| Relative controllability | Cr = | 0.887 882
|
Plots
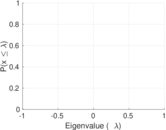
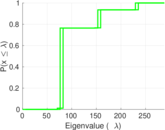
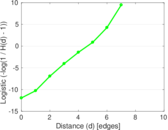
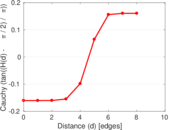
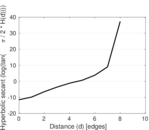
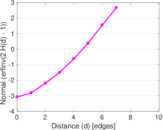
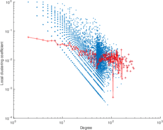
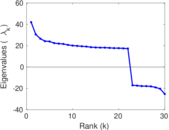
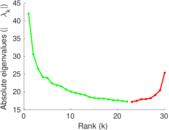
Matrix decompositions plots
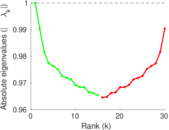
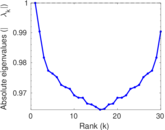
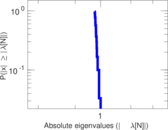
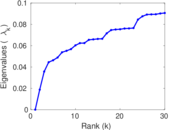
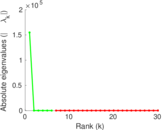
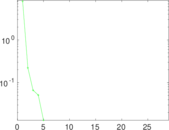
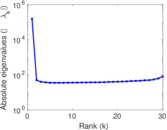
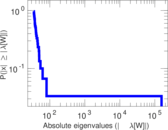
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
R. Zafarani and H. Liu.
Social computing data repository at ASU, 2009.
[ http ]
|
KONECT ‣ Networks ‣
Buy Me a Coffee
