Wikipedia edits (pt)
This is the bipartite edit network of the Portuguese Wikipedia. It contains
users and pages from the Portuguese Wikipedia, connected by edit events. Each
edge represents an edit. The dataset includes the timestamp of each edit.
Metadata
Statistics
| Size | n = | 4,784,188
|
| Left size | n1 = | 369,604
|
| Right size | n2 = | 4,414,584
|
| Volume | m = | 35,846,280
|
| Unique edge count | m̿ = | 19,502,627
|
| Wedge count | s = | 1,249,748,594,053
|
| Claw count | z = | 162,716,045,207,960,800
|
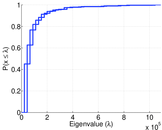
| Maximum degree | dmax = | 1,088,311
|
| Maximum left degree | d1max = | 1,088,311
|
| Maximum right degree | d2max = | 57,188
|
| Average degree | d = | 14.985 3
|
| Average left degree | d1 = | 96.985 6
|
| Average right degree | d2 = | 8.119 97
|
| Average edge multiplicity | m̃ = | 1.838 02
|
| Size of LCC | N = | 4,687,697
|
| Diameter | δ = | 13
|
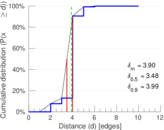
| 50-Percentile effective diameter | δ0.5 = | 3.477 20
|
| 90-Percentile effective diameter | δ0.9 = | 3.992 16
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 3.896 30
|
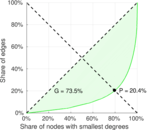
| Balanced inequality ratio | P = | 0.141 668
|
| Left balanced inequality ratio | P1 = | 0.044 094 7
|
| Right balanced inequality ratio | P2 = | 0.203 869
|
| Power law exponent | γ = | 2.265 12
|
| Tail power law exponent | γt = | 2.711 00
|
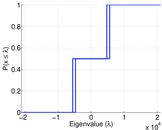
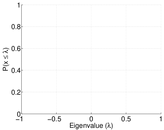
| Degree assortativity | ρ = | −0.048 976 2
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| Controllability | C = | 4,277,442
|
| Relative controllability | Cr = | 0.900 474
|
Plots
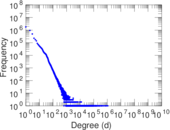
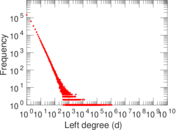
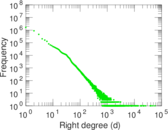
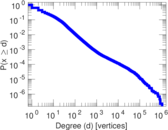
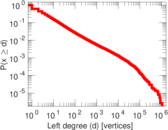
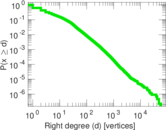
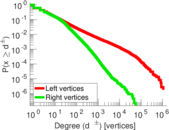
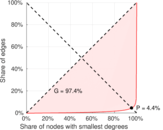
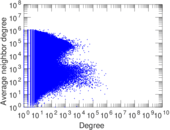
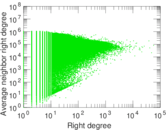
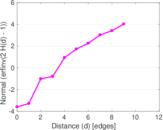
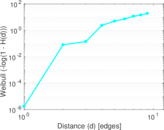
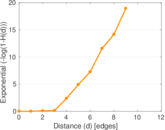
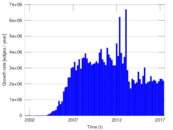
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Wikimedia Foundation.
Wikimedia downloads.
http://dumps.wikimedia.org/, January 2010.
|
KONECT ‣ Networks ‣
Buy Me a Coffee
