Facebook (NIPS)

This directed networks contains Facebook user–user friendships. A node represents a user. An edge indicates that the user represented by the left node is a friend of the user represented by the right node.

Metadata

CodeEF
Internal nameego-facebook
NameFacebook (NIPS)
Data sourcehttp://snap.stanford.edu/data/egonets-Facebook.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Online social network
Dataset timestamp 2012
Node meaningUser
Edge meaningFriendship
Network formatUnipartite, undirected
Edge typeUnweighted, no multiple edges
LoopsDoes not contain loops
Snapshot Is a snapshot and likely to not contain all data

Statistics

Size n =2,888
Volume m =2,981
Loop count l =0
Wedge count s =759,641
Claw count z =160,449,784
Cross count x =27,585,555,395
Triangle count t =91
Square count q =1,261
4-Tour count T4 =3,054,614
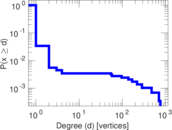
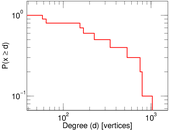
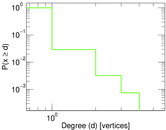
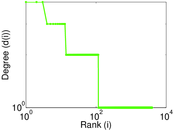
Maximum degree dmax =769
Average degree d =2.064 40
Fill p =0.000 715 069
Size of LCC N =2,888
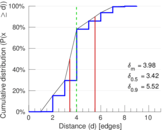
Diameter δ =9
50-Percentile effective diameter δ0.5 =3.420 92
90-Percentile effective diameter δ0.9 =5.524 62
Median distance δM =4
Mean distance δm =3.980 79
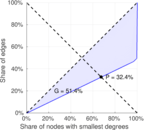
Gini coefficient G =0.514 083
Balanced inequality ratio P =0.324 388
Relative edge distribution entropy Her =0.708 747
Power law exponent γ =25.589 3
Tail power law exponent γt =4.521 00
Tail power law exponent with p γ3 =4.521 00
p-value p =0.000 00
Degree assortativity ρ =−0.668 214
Degree assortativity p-value pρ =0.000 00
Clustering coefficient c =0.000 359 380
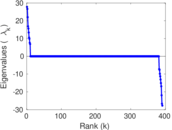
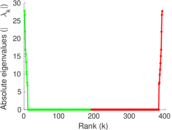
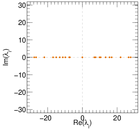
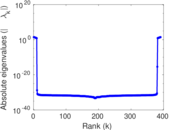
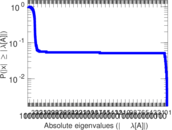
Spectral norm α =27.803 1
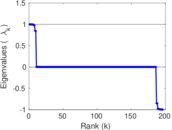
Algebraic connectivity a =0.002 377 13
Spectral separation |λ1[A] / λ2[A]| =1.002 52
Non-bipartivity bA =0.002 518 41
Normalized non-bipartivity bN =0.001 554 35
Algebraic non-bipartivity χ =0.003 114 08
Spectral bipartite frustration bK =0.000 377 116
Controllability C =2,868
Relative controllability Cr =0.993 075

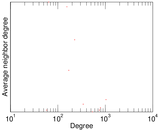
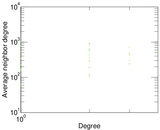
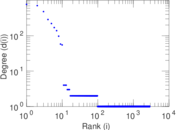
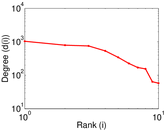
Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

In/outdegree scatter plot

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

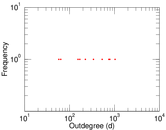
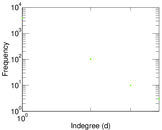
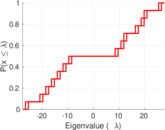
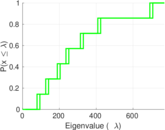
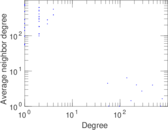
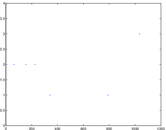
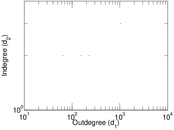
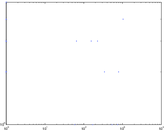
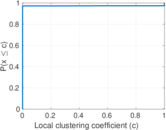
Matrix decompositions plots

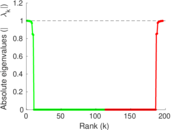
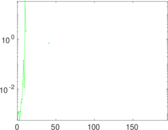
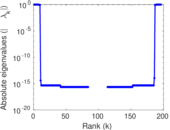
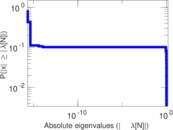
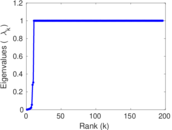
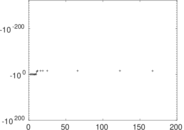
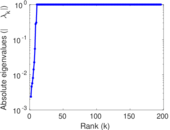
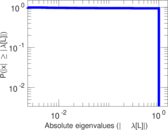
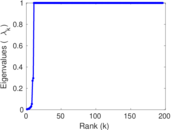
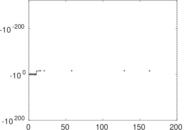
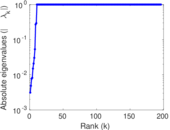
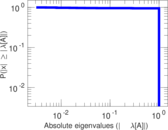
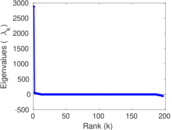
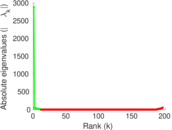
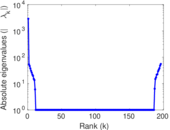
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Julian McAuley and Jure Leskovec. Learning to discover social circles in ego networks. In Adv. in Neural Inf. Process. Syst., pages 548–556. 2012.