EU institution
This is the email communication network of a large, undisclosed European
institution. Nodes represent individual persons. Edges between two persons are
directed and denote that at least one email has been sent from one person to
the other. All edges are simple: Even if a person has sent multiple emails to
another person, the two persons will be connected only by a single edge in that
direction. Spam emails have been removed from the dataset.
Metadata
Statistics
| Size | n = | 265,214
|
| Volume | m = | 420,045
|
| Loop count | l = | 1,089
|
| Wedge count | s = | 195,288,557
|
| Claw count | z = | 250,257,426,117
|
| Cross count | x = | 330,517,523,039,094
|
| Triangle count | t = | 267,313
|
| Square count | q = | 18,421,946
|
| 4-Tour count | T4 = | 929,258,758
|
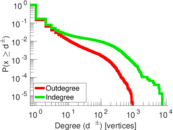
| Maximum degree | dmax = | 7,636
|
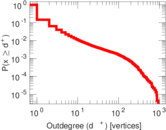
| Maximum outdegree | d+max = | 930
|
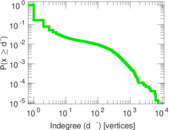
| Maximum indegree | d−max = | 7,631
|
| Average degree | d = | 3.167 59
|
| Fill | p = | 5.971 77 × 10−6
|
| Size of LCC | N = | 224,832
|
| Size of LSCC | Ns = | 34,203
|
| Relative size of LSCC | Nrs = | 0.128 964
|
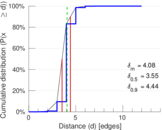
| Diameter | δ = | 14
|
| 50-Percentile effective diameter | δ0.5 = | 3.549 11
|
| 90-Percentile effective diameter | δ0.9 = | 4.439 88
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 4.080 16
|
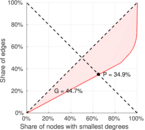
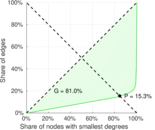
| Gini coefficient | G = | 0.663 243
|
| Balanced inequality ratio | P = | 0.239 929
|
| Outdegree balanced inequality ratio | P+ = | 0.348 808
|
| Indegree balanced inequality ratio | P− = | 0.152 931
|
| Relative edge distribution entropy | Her = | 0.798 488
|
| Power law exponent | γ = | 6.649 66
|
| Tail power law exponent | γt = | 2.931 00
|
| Tail power law exponent with p | γ3 = | 2.931 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 2.971 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 2.661 00
|
| Indegree p-value | pi = | 0.000 00
|
| Degree assortativity | ρ = | −0.178 125
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.145 893
|
| Clustering coefficient | c = | 0.004 106 43
|
| Directed clustering coefficient | c± = | 0.014 716 4
|
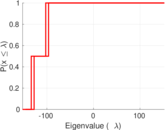
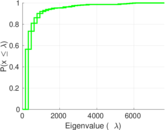
| Spectral norm | α = | 152.046
|
| Operator 2-norm | ν = | 87.357 1
|
| Cyclic eigenvalue | π = | 69.932 3
|
| Algebraic connectivity | a = | 0.000 202 791
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.602 95
|
| Reciprocity | y = | 0.261 970
|
| Non-bipartivity | bA = | 0.425 255
|
| Normalized non-bipartivity | bN = | 9.817 48 × 10−5
|
| Algebraic non-bipartivity | χ = | 0.000 196 327
|
| Spectral bipartite frustration | bK = | 1.619 03 × 10−5
|
| Controllability | C = | 245,791
|
| Relative controllability | Cr = | 0.926 765
|
Plots

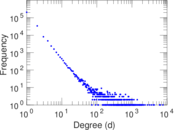
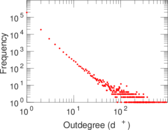
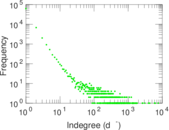
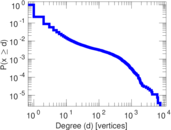


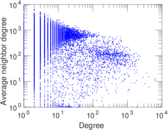
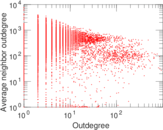
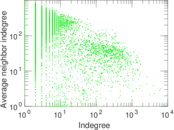
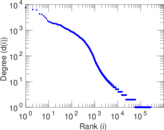
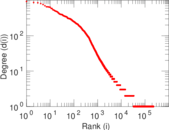
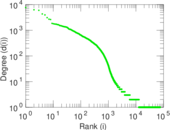





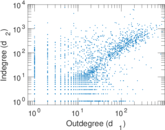
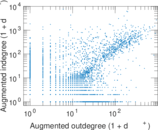
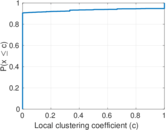
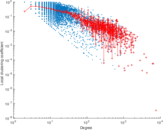
Matrix decompositions plots
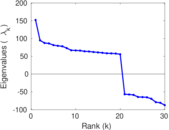
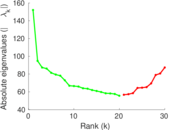
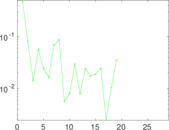

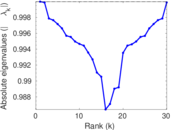
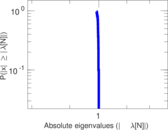
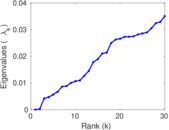
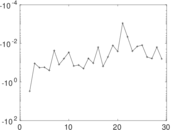
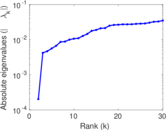
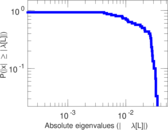
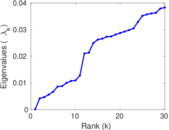
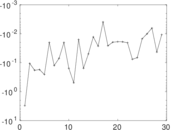
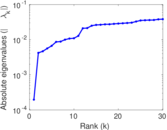
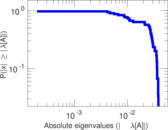
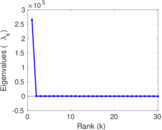
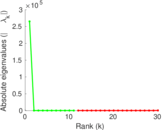
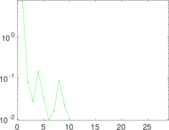
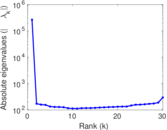
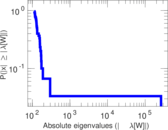
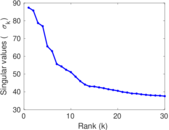
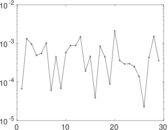
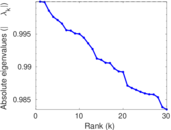
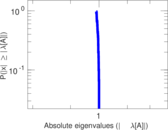
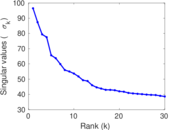
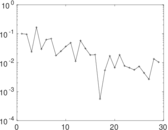
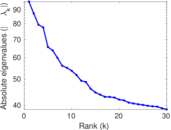
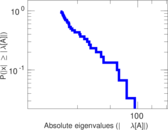
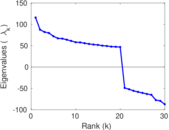
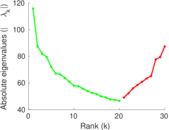
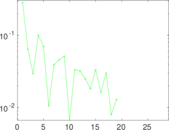
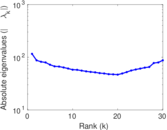

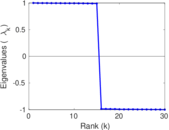
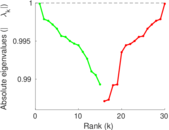
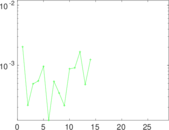

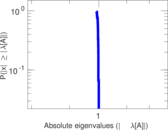
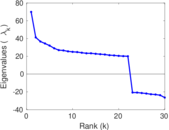
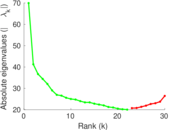
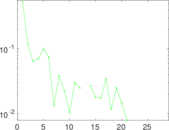
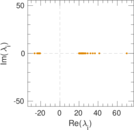
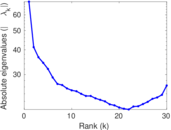
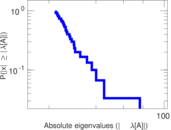
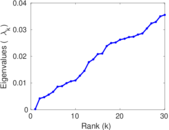
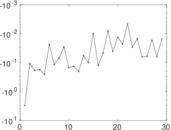
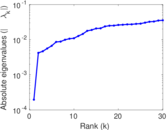
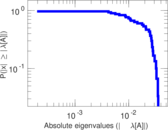
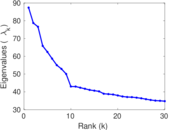
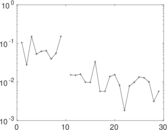
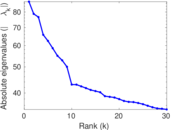
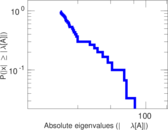
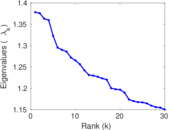
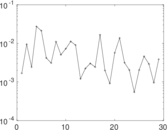
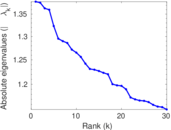
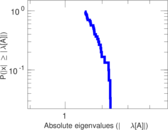
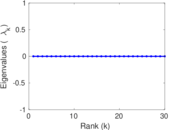
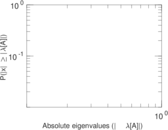
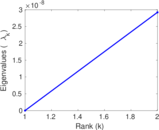
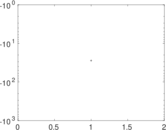
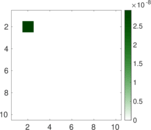
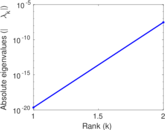

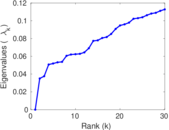
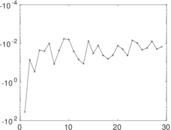
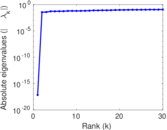

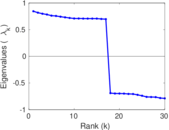
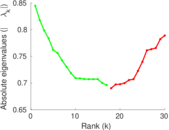
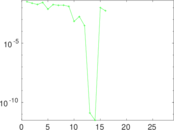
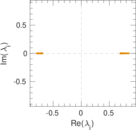

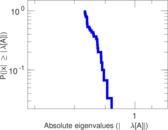
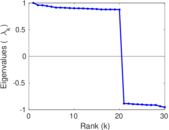
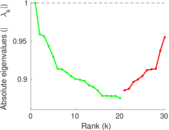
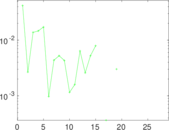
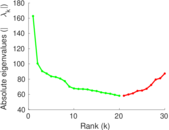
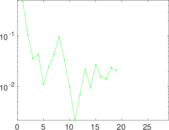
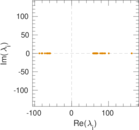
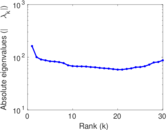
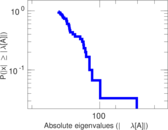
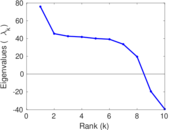
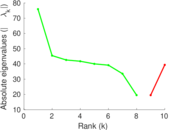
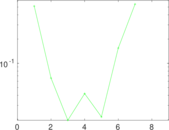
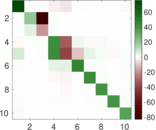
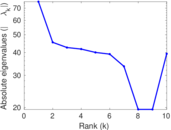
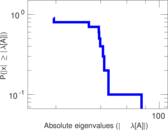
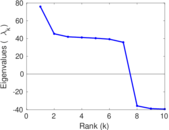
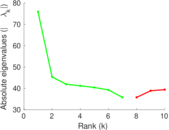
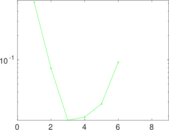
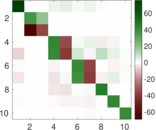
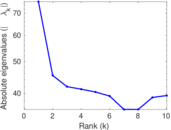
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Jure Leskovec, Jon Kleinberg, and Christos Faloutsos.
Graph evolution: Densification and shrinking diameters.
ACM Trans. Knowl. Discov. from Data, 1(1):1–40, 2007.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee






















































































































































