Flickr links

This is the social network of Flickr users and their connections. The network is undirected. The dataset was crawled

Metadata

CodeLF
Internal nameflickr-links
NameFlickr links
Data sourcehttp://socialnetworks.mpi-sws.org/data-imc2007.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Online social network
Dataset timestamp 2007
Node meaningUser
Edge meaningLink
Network formatUnipartite, undirected
Edge typeUnweighted, no multiple edges
LoopsContains loops
Snapshot Is a snapshot and likely to not contain all data

Statistics

Size n =1,715,255
Volume m =15,551,250
Loop count l =1
Wedge count s =14,660,775,057
Claw count z =21,493,389,022,491
Cross count x =61,068,223,891,975,320
Triangle count t =548,174,465
Square count q =428,125,008,285
4-Tour count T4 =3,483,825,597,342
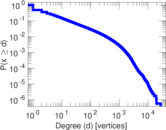
Maximum degree dmax =27,224
Average degree d =18.132 9
Fill p =1.057 15 × 10−5
Size of LCC N =1,624,991
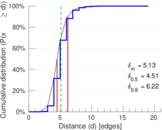
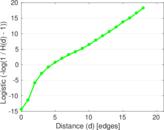
Diameter δ =24
50-Percentile effective diameter δ0.5 =4.510 39
90-Percentile effective diameter δ0.9 =6.218 59
Median distance δM =5
Mean distance δm =5.127 45
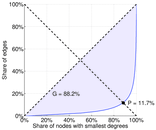
Gini coefficient G =0.882 436
Balanced inequality ratio P =0.116 856
Relative edge distribution entropy Her =0.822 037
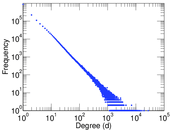
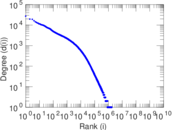
Power law exponent γ =2.039 66
Tail power law exponent γt =1.731 00
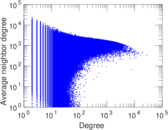
Degree assortativity ρ =−0.015 278 6
Degree assortativity p-value pρ =0.000 00
Clustering coefficient c =0.112 172
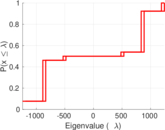
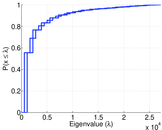
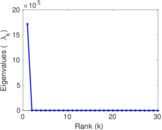
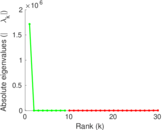
Spectral norm α =1,240.26
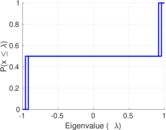
Spectral separation |λ1[A] / λ2[A]| =1.355 68
Non-bipartivity bA =0.674 071
Normalized non-bipartivity bN =0.001 850 47
Algebraic non-bipartivity χ =0.003 650 23
Spectral bipartite frustration bK =4.791 87 × 10−5

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Clustering coefficient distribution

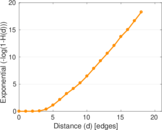
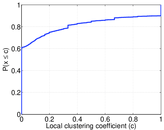
Matrix decompositions plots

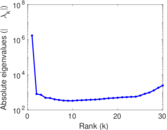
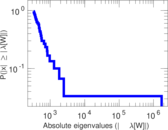
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Alan Mislove, Massimiliano Marcon, Krishna P. Gummadi, Peter Druschel, and Bobby Bhattacharjee. Measurement and analysis of online social networks. In Proc. Internet Measurement Conf., 2007.