Wikipedia dynamic (it)

This network shows the evolution of hyperlinks between articles of the Italian Wikipedia. The nodes represent articles. An edge indicates that a hyperlink was added or removed depending on the edge weight (−1 for removal or +1 for addition).

Metadata

CodeUi
Internal namelink-dynamic-itwiki
NameWikipedia dynamic (it)
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Hyperlink network
Node meaningArticle
Edge meaningReference
Network formatUnipartite, directed
Edge typeDynamic
Temporal data Edges are annotated with timestamps
ReciprocalContains reciprocal edges
Directed cyclesContains directed cycles
LoopsContains loops

Statistics

Size n =1,204,009
Volume m =34,826,283
Unique edge count m̿ =17,086,845
Loop count l =1,270
Wedge count s =58,316,691,930
Claw count z =376,622,699,709,806
Cross count x =4,154,912,852,663,083,008
Triangle count t =98,571,145
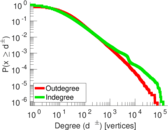
Maximum degree dmax =140,949
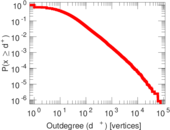
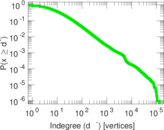
Maximum outdegree d+max =76,631
Maximum indegree d−max =131,066
Average degree d =57.850 5
Fill p =1.184 83 × 10−5
Average edge multiplicity m̃ =2.038 19
Size of LCC N =1,202,469
Size of LSCC Ns =920,293
Relative size of LSCC Nrs =0.764 357
Diameter δ =16
50-Percentile effective diameter δ0.5 =3.121 06
90-Percentile effective diameter δ0.9 =4.200 78
Median distance δM =4
Mean distance δm =3.650 98
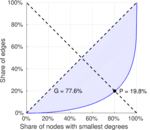
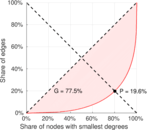
Gini coefficient G =0.735 612
Balanced inequality ratio P =0.216 412
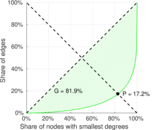
Outdegree balanced inequality ratio P+ =0.230 946
Indegree balanced inequality ratio P− =0.184 752
Relative edge distribution entropy Her =0.887 405
Power law exponent γ =1.481 98
Tail power law exponent γt =2.411 00
Degree assortativity ρ =−0.074 786 8
Degree assortativity p-value pρ =0.000 00
Clustering coefficient c =0.005 070 82
Directed clustering coefficient c± =0.034 316 4
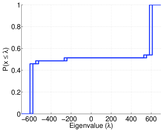
Spectral norm α =696.272
Operator 2-norm ν =621.980
Cyclic eigenvalue π =117.805
Reciprocity y =0.150 004
Non-bipartivity bA =0.171 205
Normalized non-bipartivity bN =0.019 282 9

Plots

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Hop distribution

In/outdegree scatter plot

Average neighbor degree distribution

Temporal distribution

Signed temporal distribution

Inter-event distribution

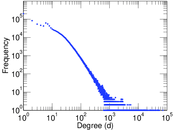
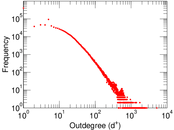
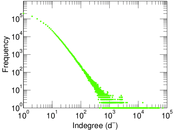
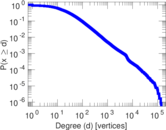
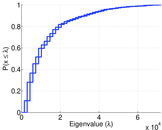
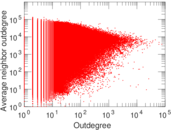
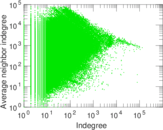
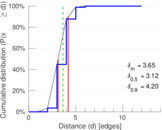
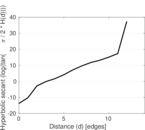
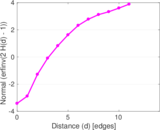
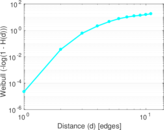
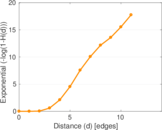
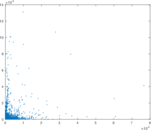
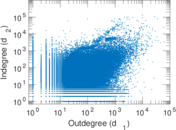
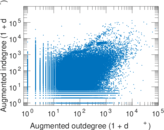
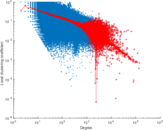
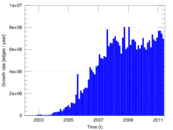
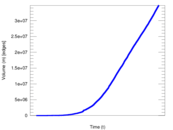
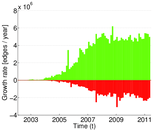
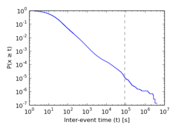
Matrix decompositions plots

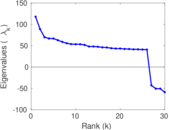
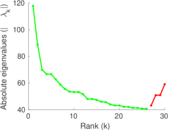
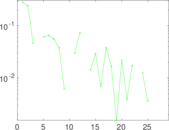
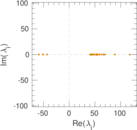
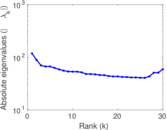
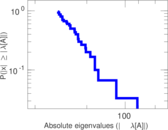
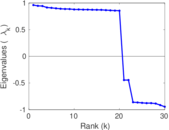
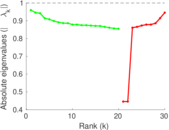
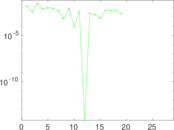
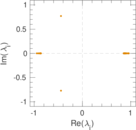
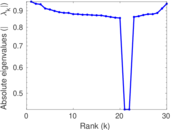
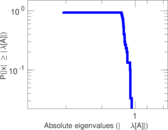
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Julia Preusse, Jérôme Kunegis, Matthias Thimm, Thomas Gottron, and Steffen Staab. Structural dynamics of knowledge networks. In Proc. Int. Conf. on Weblogs and Soc. Media, 2013.