Brightkite

This undirected network contains user–user friendship relations from Brightkite, a former location-based social network were user shared their locations. A node represents a user and an edge indicates that a friendship exists between the user represented by the left node and the user represented by the right node.

Metadata

CodeBK
Internal nameloc-brightkite_edges
NameBrightkite
Data sourcehttp://snap.stanford.edu/data/loc-brightkite.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Online social network
Dataset timestamp 2011
Node meaningUser
Edge meaningFriendship
Network formatUnipartite, undirected
Edge typeUnweighted, no multiple edges
LoopsDoes not contain loops

Statistics

Size n =58,228
Volume m =214,078
Loop count l =0
Wedge count s =13,423,403
Claw count z =1,455,808,231
Cross count x =248,701,890,895
Triangle count t =494,728
Square count q =23,380,701
4-Tour count T4 =241,167,376
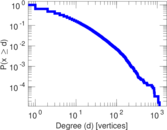
Maximum degree dmax =1,134
Average degree d =7.353 09
Fill p =0.000 126 283
Size of LCC N =56,739
Diameter δ =18
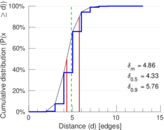
50-Percentile effective diameter δ0.5 =4.331 65
90-Percentile effective diameter δ0.9 =5.764 94
Median distance δM =5
Mean distance δm =4.859 34
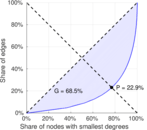
Gini coefficient G =0.684 989
Balanced inequality ratio P =0.229 288
Relative edge distribution entropy Her =0.902 235
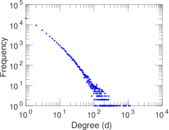
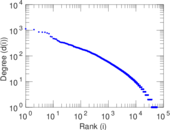
Power law exponent γ =1.905 79
Tail power law exponent γt =2.481 00
Tail power law exponent with p γ3 =2.481 00
p-value p =0.000 00
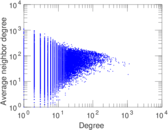
Degree assortativity ρ =+0.010 815 8
Degree assortativity p-value pρ =1.469 32 × 10−12
Clustering coefficient c =0.110 567
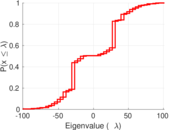
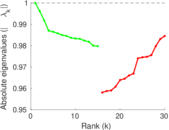
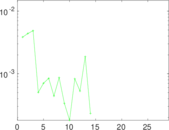
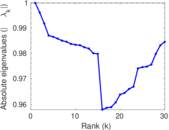
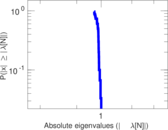
Spectral norm α =101.491
Algebraic connectivity a =0.028 857 7
Spectral separation |λ1[A] / λ2[A]| =1.305 74
Non-bipartivity bA =0.650 823
Normalized non-bipartivity bN =0.015 484 9
Algebraic non-bipartivity χ =0.028 871 0
Spectral bipartite frustration bK =0.000 961 582
Controllability C =15,728
Relative controllability Cr =0.270 111

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

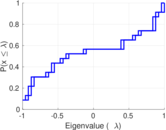
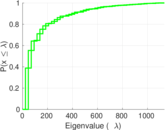
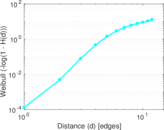
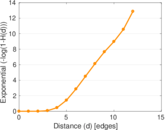
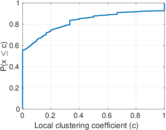
Matrix decompositions plots

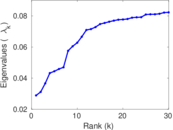
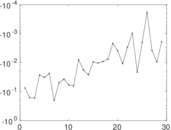
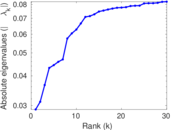
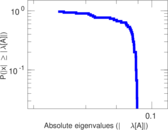
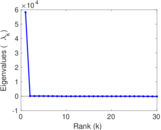
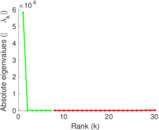
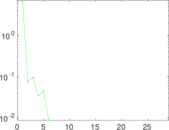
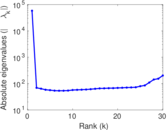
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Eunjoon Cho, Seth A. Myers, and Jure Leskovec. Friendship and mobility: User movement in location-based social networks. In Proc. Int. Conf. on Knowl. Discov. and Data Min., pages 1082–1090, 2011.