Gowalla

This undirected network contains user–user friendship relations from Gowalla, a former location-based social network where user shared their locations. A node represents a user and an edge indicates that a friendship exists between the user represented by the left node and the user represented by the right node.

Metadata

CodeGW
Internal nameloc-gowalla_edges
NameGowalla
Data sourcehttp://snap.stanford.edu/data/loc-gowalla.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Online social network
Dataset timestamp 2012
Node meaningUser
Edge meaningFriendship
Network formatUnipartite, undirected
Edge typeUnweighted, no multiple edges
LoopsDoes not contain loops

Statistics

Size n =196,591
Volume m =950,327
Loop count l =0
Wedge count s =290,400,040
Claw count z =787,564,904,976
Cross count x =2,482,179,360,928,230
Triangle count t =2,273,138
Square count q =146,652,712
4-Tour count T4 =2,336,722,510
Maximum degree dmax =14,730
Average degree d =9.668 06
Fill p =4.917 88 × 10−5
Size of LCC N =196,591
Diameter δ =16
50-Percentile effective diameter δ0.5 =3.857 66
90-Percentile effective diameter δ0.9 =5.350 12
Median distance δM =4
Mean distance δm =4.426 42
Gini coefficient G =0.683 353
Balanced inequality ratio P =0.235 012
Relative edge distribution entropy Her =0.904 326
Power law exponent γ =1.730 70
Tail power law exponent γt =2.651 00
Tail power law exponent with p γ3 =2.651 00
p-value p =0.000 00
Degree assortativity ρ =−0.029 254 7
Degree assortativity p-value pρ =0.000 00
Clustering coefficient c =0.023 482 8
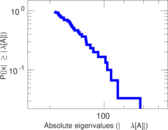
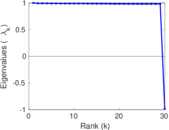
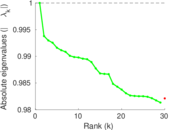
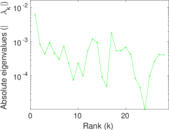
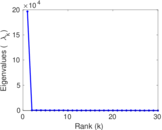
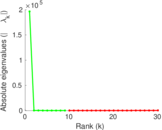
Spectral norm α =170.939
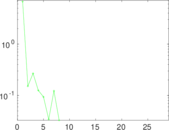
Algebraic connectivity a =0.021 547 2
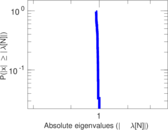
Spectral separation |λ1[A] / λ2[A]| =1.395 92
Non-bipartivity bA =0.283 628
Normalized non-bipartivity bN =0.017 892 4
Algebraic non-bipartivity χ =0.033 180 9
Spectral bipartite frustration bK =0.000 858 003
Controllability C =36,679
Relative controllability Cr =0.186 575

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Delaunay graph drawing

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

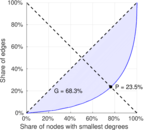
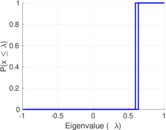
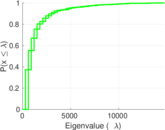
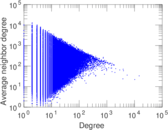
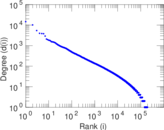
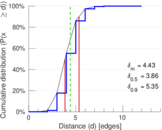
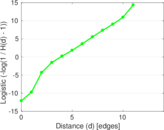
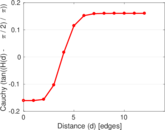
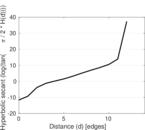
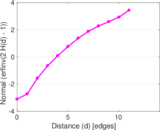
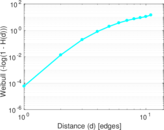
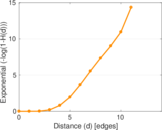
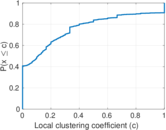
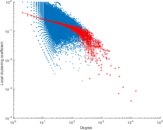
Matrix decompositions plots

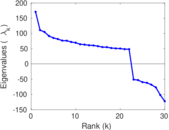
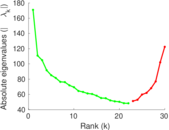
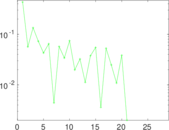
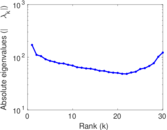
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Eunjoon Cho, Seth A. Myers, and Jure Leskovec. Friendship and mobility: User movement in location-based social networks. In Proc. Int. Conf. on Knowl. Discov. and Data Min., pages 1082–1090, 2011.