Human proteins (Stelzl)

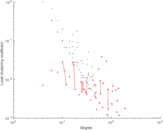
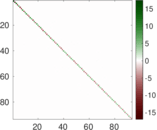
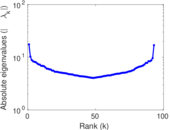
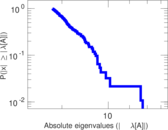
This network represens interacting pairs of protein in Humans (Homo sapiens).

Metadata

CodeMS
Internal namemaayan-Stelzl
NameHuman proteins (Stelzl)
Data sourcehttp://research.mssm.edu/maayan/datasets/qualitative_networks.shtml
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Metabolic network
Node meaningProtein
Edge meaningInteraction
Network formatUnipartite, directed
Edge typeUnweighted, no multiple edges
ReciprocalContains reciprocal edges
Directed cyclesContains directed cycles
LoopsContains loops

Statistics

Size n =1,706
Volume m =6,207
Loop count l =36
Wedge count s =49,920
Claw count z =5,644,533
Cross count x =164,829,932
Triangle count t =96
Square count q =15,969
4-Tour count T4 =333,742
Maximum degree dmax =189
Maximum outdegree d+max =95
Maximum indegree d−max =94
Average degree d =7.276 67
Fill p =0.002 132 67
Size of LCC N =1,615
Size of LSCC Ns =1,493
Relative size of LSCC Nrs =0.875 147
Diameter δ =13
50-Percentile effective diameter δ0.5 =4.369 98
90-Percentile effective diameter δ0.9 =6.972 38
Median distance δM =5
Mean distance δm =5.093 13
Gini coefficient G =0.588 845
Balanced inequality ratio P =0.271 307
Outdegree balanced inequality ratio P+ =0.276 301
Indegree balanced inequality ratio P− =0.276 301
Relative edge distribution entropy Her =0.898 391
Power law exponent γ =2.354 17
Tail power law exponent γt =2.381 00
Tail power law exponent with p γ3 =2.381 00
p-value p =0.228 000
Outdegree tail power law exponent with p γ3,o =2.381 00
Outdegree p-value po =0.141 000
Indegree tail power law exponent with p γ3,i =2.411 00
Indegree p-value pi =0.105 000
Degree assortativity ρ =−0.191 596
Degree assortativity p-value pρ =3.080 74 × 10−53
In/outdegree correlation ρ± =+0.968 049
Clustering coefficient c =0.005 769 23
Directed clustering coefficient c± =0.005 933 86
Spectral norm α =35.012 4
Operator 2-norm ν =17.514 0
Cyclic eigenvalue π =17.498 7
Algebraic connectivity a =0.051 258 6
Spectral separation |λ1[A] / λ2[A]| =1.033 34
Reciprocity y =0.977 606
Non-bipartivity bA =0.032 266 0
Normalized non-bipartivity bN =0.011 883 7
Algebraic non-bipartivity χ =0.025 524 6
Spectral bipartite frustration bK =0.001 643 11
Controllability C =771
Relative controllability Cr =0.451 934

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

In/outdegree scatter plot

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

Matrix decompositions plots

Downloads

References

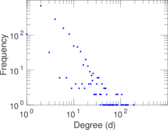
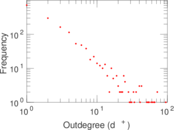
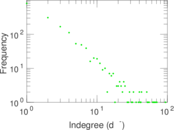
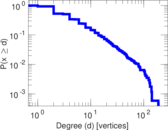
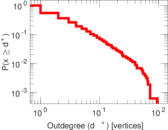
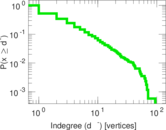
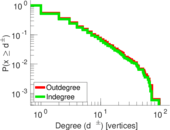
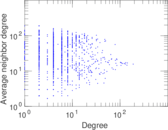
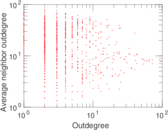
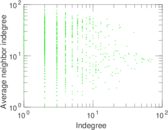
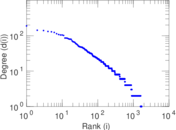
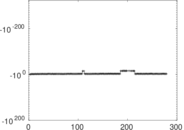
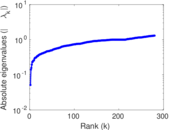
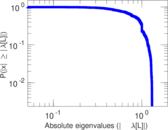
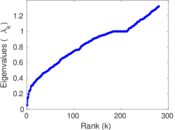
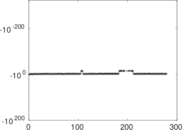
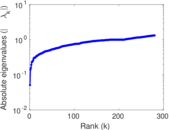
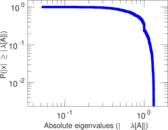
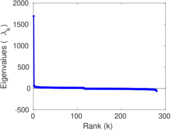
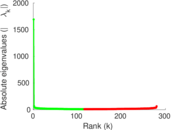
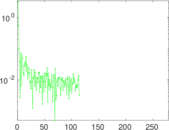
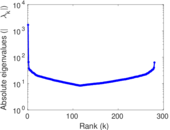
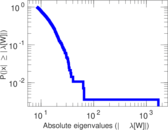
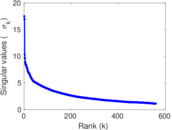
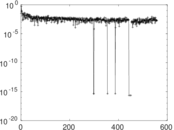
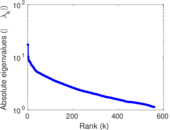
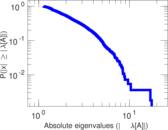
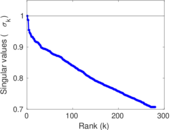
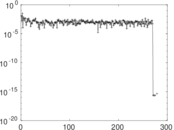
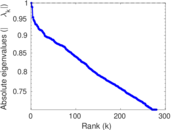
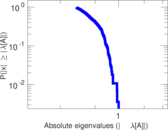
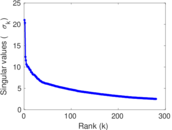
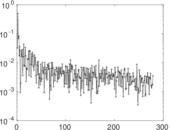
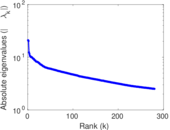
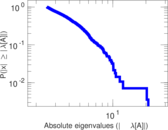
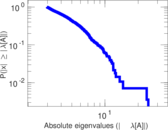
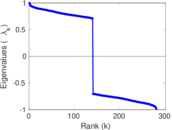
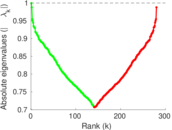
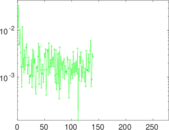
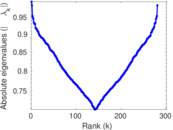
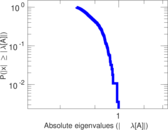
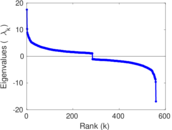
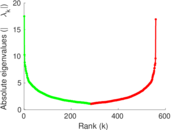
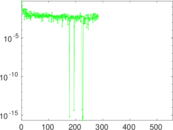
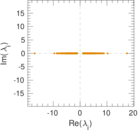
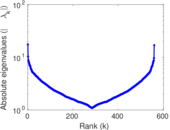
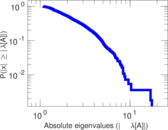
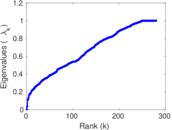
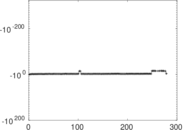
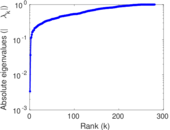
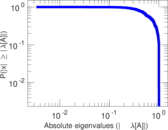
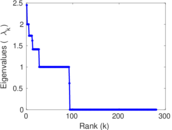
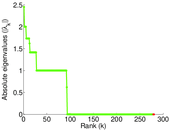
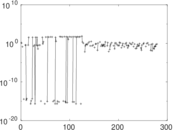
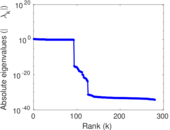
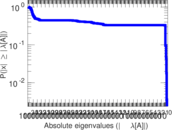
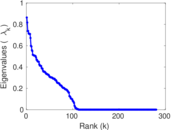
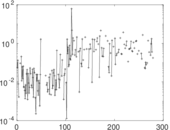
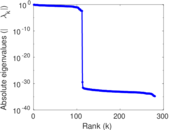
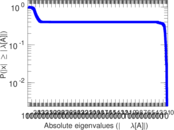
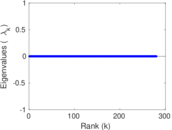
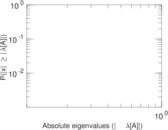
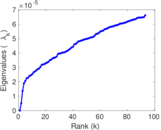
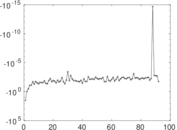
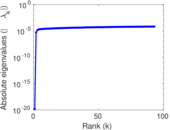
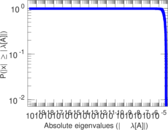
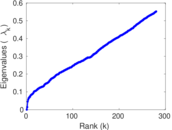
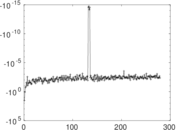
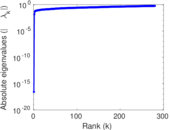
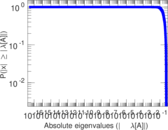
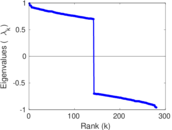
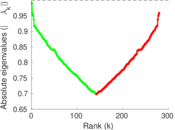
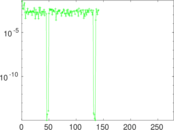
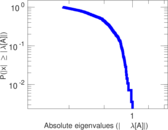
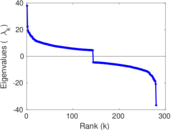
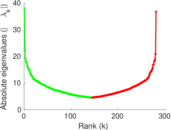
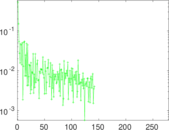
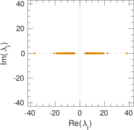
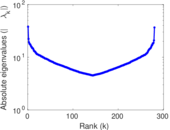
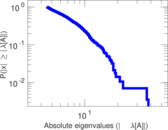
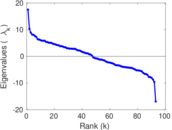
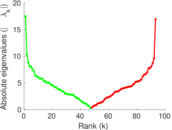
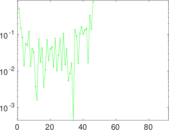
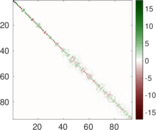
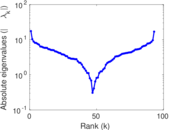
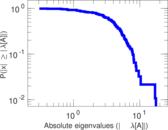
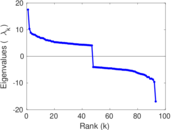
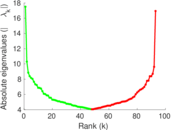
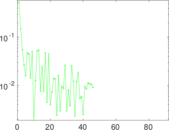
[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] U. Stelzl, U. Worm, M. Lalowski, C. Haenig, F. H. Brembeck, H. Goehler, M. Stroedicke, M. Zenkner, A. Schoenherr, S. Koeppen, J. Timm, S. Mintzlaff, C. Abraham, N. Bock, S. Kietzmann, A. Goedde, E Toksöz, A. Droege, S. Krobitsch, B. Korn, W. Birchmeier, H. Lehrach, and E. E. Wanker. A human protein–protein interaction network: A resource for annotating the proteome. Cell, 122:957–968, 2005.