Marvel
This is the fictional collaboration network of characters in works of Marvel, a
publisher of comic books based in the United States of America. The network is
bipartite. Nodes are characters and works, and an edge is present when a
character appears in a work. The dataset takes works only into account if thy
were published starting in 1961. To cite the paper: "We only consider here
comics published after Issue 1 of Fantastic Four (dated November 1961), which
is understood as the point of departure of the Marvel Age of Comics." The data
was extracted from the Marvel Chronology Project (MCP) created by Russ Chappell
(www.chronologyproject.com). The dataset does contain the names of the
characters, even though a few a empty strings.
Metadata
Statistics
| Size | n = | 25,914
|
| Left size | n1 = | 6,486
|
| Right size | n2 = | 19,428
|
| Volume | m = | 96,662
|
| Wedge count | s = | 12,869,214
|
| Claw count | z = | 3,054,666,860
|
| Cross count | x = | 795,147,934,751
|
| Triangle count | t = | 0
|
| Square count | q = | 10,709,594
|
| 4-Tour count | T4 = | 137,346,932
|
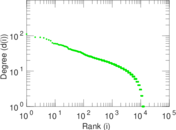
| Maximum degree | dmax = | 1,625
|
| Maximum left degree | d1max = | 1,625
|
| Maximum right degree | d2max = | 111
|
| Average degree | d = | 7.460 21
|
| Average left degree | d1 = | 14.903 2
|
| Average right degree | d2 = | 4.975 40
|
| Fill | p = | 0.000 767 098
|
| Size of LCC | N = | 19,365
|
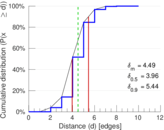
| Diameter | δ = | 11
|
| 50-Percentile effective diameter | δ0.5 = | 3.955 58
|
| 90-Percentile effective diameter | δ0.9 = | 5.442 45
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 4.491 85
|
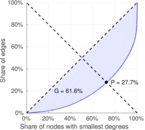
| Gini coefficient | G = | 0.615 843
|
| Balanced inequality ratio | P = | 0.276 929
|
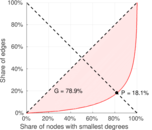
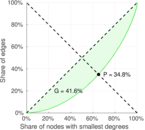
| Left balanced inequality ratio | P1 = | 0.181 385
|
| Right balanced inequality ratio | P2 = | 0.347 541
|
| Relative edge distribution entropy | Her = | 0.895 614
|
| Power law exponent | γ = | 1.635 85
|
| Tail power law exponent | γt = | 2.181 00
|
| Tail power law exponent with p | γ3 = | 2.181 00
|
| p-value | p = | 0.049 000 0
|
| Left tail power law exponent with p | γ3,1 = | 1.951 00
|
| Left p-value | p1 = | 0.009 000 00
|
| Right tail power law exponent with p | γ3,2 = | 4.681 00
|
| Right p-value | p2 = | 0.029 000 0
|
| Degree assortativity | ρ = | −0.017 701 3
|
| Degree assortativity p-value | pρ = | 3.717 11 × 10−8
|
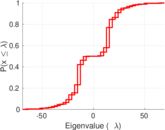
| Spectral norm | α = | 69.136 5
|
| Algebraic connectivity | a = | 0.042 315 6
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.290 64
|
| Controllability | C = | 9,364
|
| Relative controllability | Cr = | 0.481 985
|
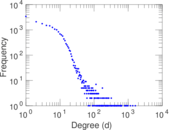
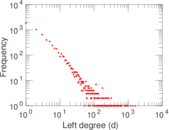
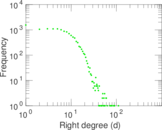
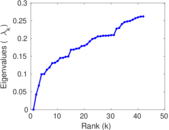
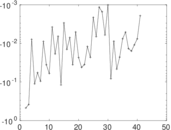
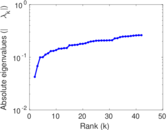
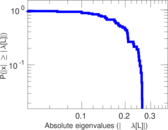
Plots

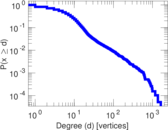
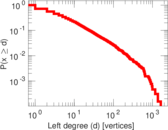
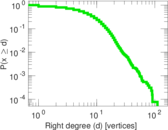
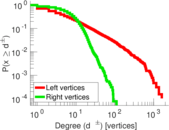
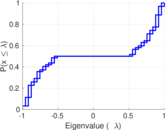
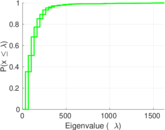


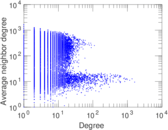
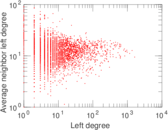
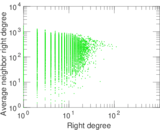
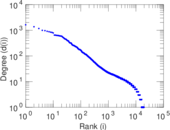
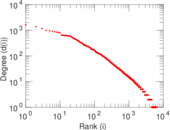
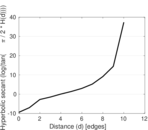
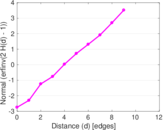
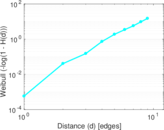
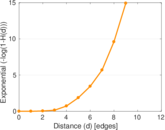




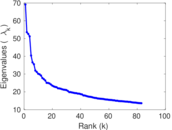
Matrix decompositions plots
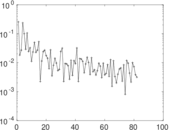
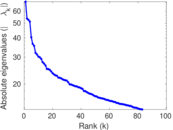
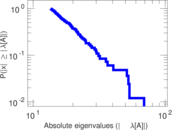

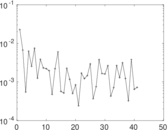
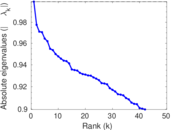
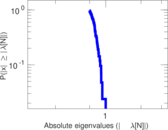
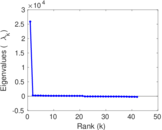
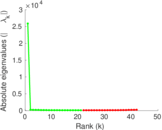
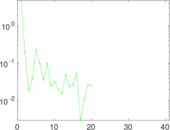
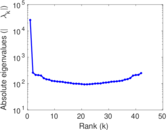
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Ricardo Alberich, J. Miro-Julia, and Francesc Rosselló.
Marvel universe looks almost like a real social network.
2002.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee