Residence hall
This directed network contains friendship ratings between 217 residents living
at a residence hall located on the Australian National University campus. A
node represents a person and
Metadata
Statistics
| Size | n = | 217
|
| Volume | m = | 2,672
|
| Loop count | l = | 0
|
| Wedge count | s = | 35,859
|
| Claw count | z = | 848,578
|
| Cross count | x = | 8,287,727
|
| Triangle count | t = | 3,629
|
| Square count | q = | 35,657
|
| 4-Tour count | T4 = | 432,370
|
| Maximum degree | dmax = | 80
|
| Maximum outdegree | d+max = | 51
|
| Maximum indegree | d−max = | 34
|
| Average degree | d = | 24.626 7
|
| Fill | p = | 0.057 006 3
|
| Size of LCC | N = | 217
|
| Size of LSCC | Ns = | 214
|
| Relative size of LSCC | Nrs = | 0.986 175
|
| Diameter | δ = | 4
|
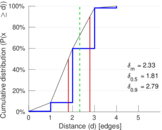
| 50-Percentile effective diameter | δ0.5 = | 1.807 59
|
| 90-Percentile effective diameter | δ0.9 = | 2.785 73
|
| Median distance | δM = | 2
|
| Mean distance | δm = | 2.327 48
|
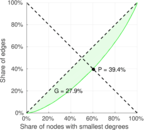
| Gini coefficient | G = | 0.244 081
|
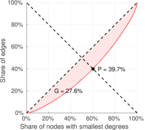
| Balanced inequality ratio | P = | 0.408 121
|
| Outdegree balanced inequality ratio | P+ = | 0.397 081
|
| Indegree balanced inequality ratio | P− = | 0.393 713
|
| Relative edge distribution entropy | Her = | 0.981 563
|
| Power law exponent | γ = | 1.492 83
|
| Tail power law exponent | γt = | 6.321 00
|
| Tail power law exponent with p | γ3 = | 6.321 00
|
| p-value | p = | 0.942 000
|
| Outdegree tail power law exponent with p | γ3,o = | 4.601 00
|
| Outdegree p-value | po = | 0.317 000
|
| Indegree tail power law exponent with p | γ3,i = | 8.911 00
|
| Indegree p-value | pi = | 0.584 000
|
| Degree assortativity | ρ = | +0.095 962 5
|
| Degree assortativity p-value | pρ = | 5.500 55 × 10−9
|
| In/outdegree correlation | ρ± = | +0.480 021
|
| Clustering coefficient | c = | 0.303 606
|
| Directed clustering coefficient | c± = | 0.302 612
|
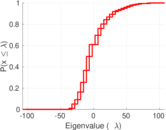
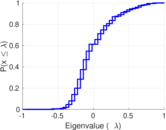
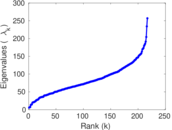
| Spectral norm | α = | 107.958
|
| Operator 2-norm | ν = | 57.034 8
|
| Cyclic eigenvalue | π = | 50.874 7
|
| Algebraic connectivity | a = | 5.353 63
|
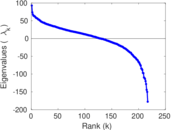
| Spectral separation | |λ1[A] / λ2[A]| = | 1.315 62
|
| Reciprocity | y = | 0.623 503
|
| Non-bipartivity | bA = | 0.664 996
|
| Normalized non-bipartivity | bN = | 0.572 754
|
| Algebraic non-bipartivity | χ = | 1.783 97
|
| Spectral bipartite frustration | bK = | 0.026 313 3
|
| Controllability | C = | 2
|
| Relative controllability | Cr = | 0.009 216 59
|
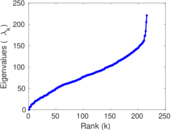
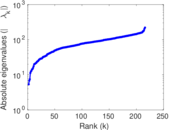
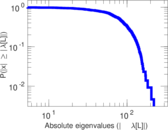
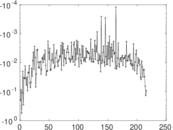
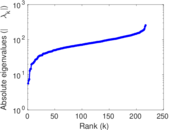
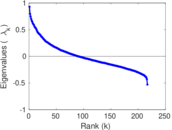
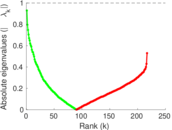
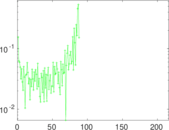
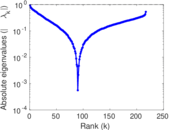
Plots

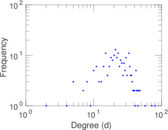
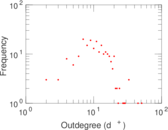
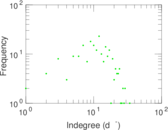
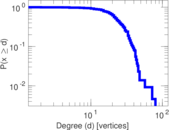
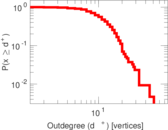
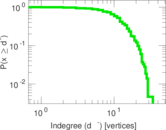
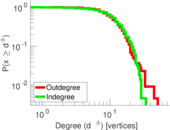
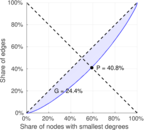
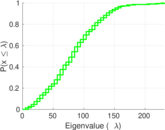


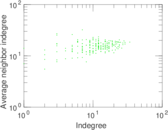
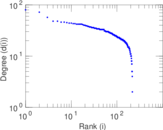
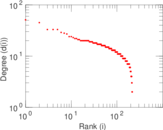
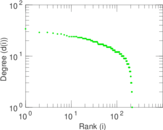
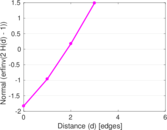
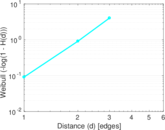
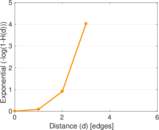

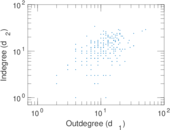
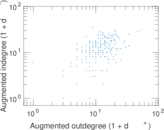
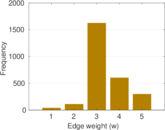
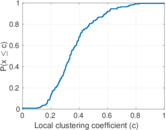
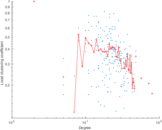
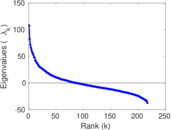
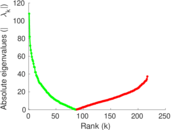
Matrix decompositions plots
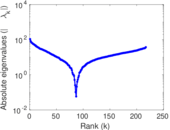
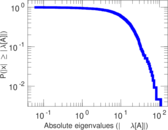
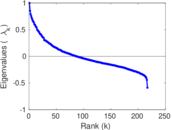
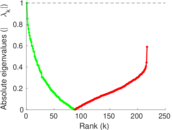
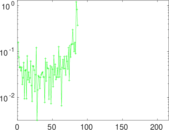
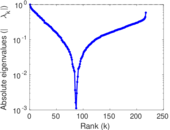
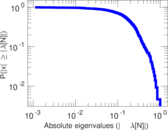

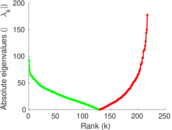
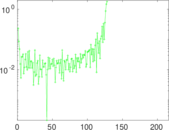
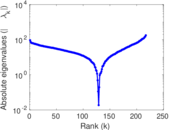
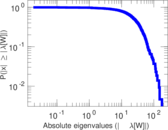
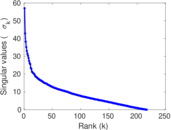
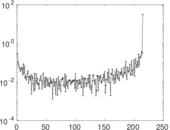
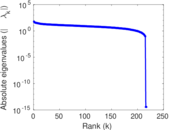
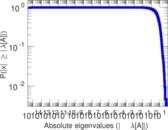
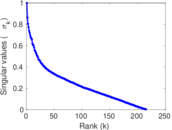
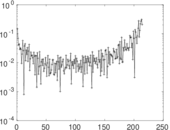
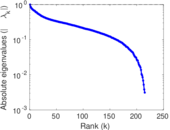
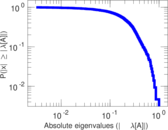
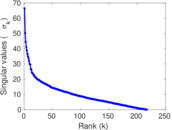

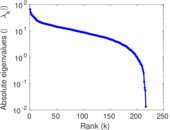
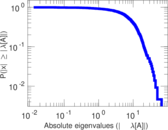
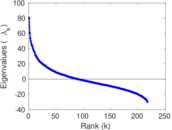
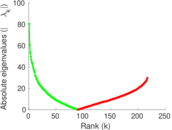
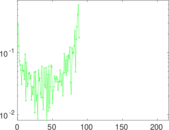
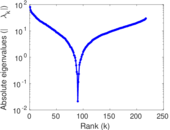
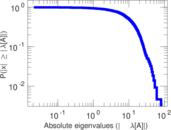
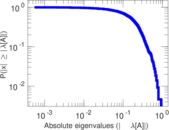
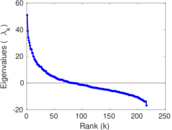
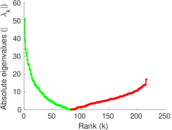
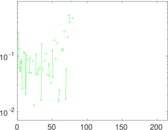
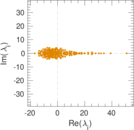
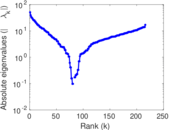
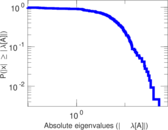
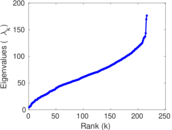
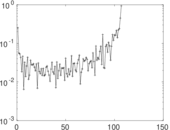
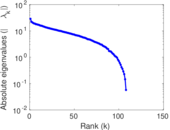
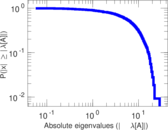
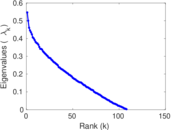
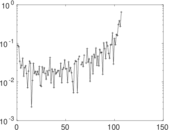
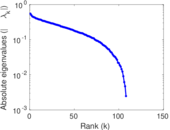
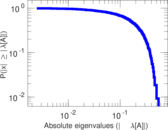
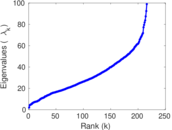
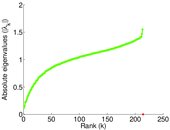
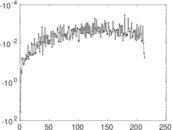
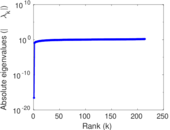

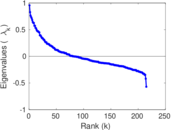
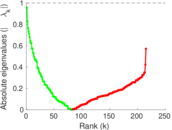
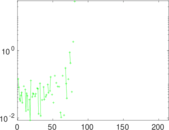
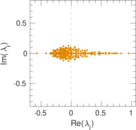
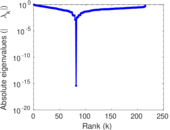
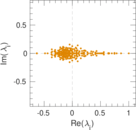
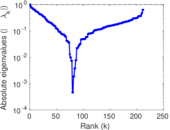
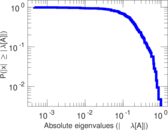
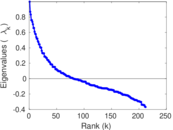
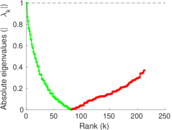
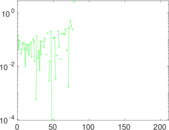
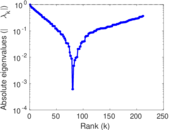
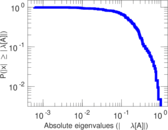
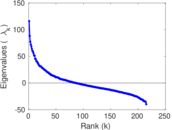
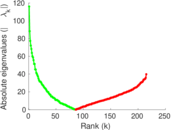
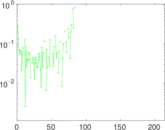
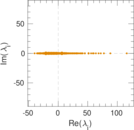
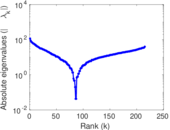
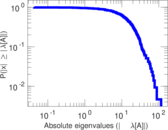
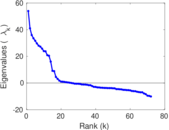

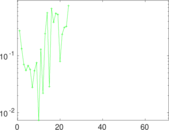
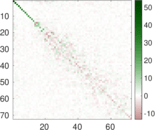
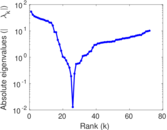
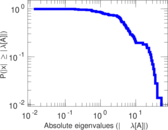
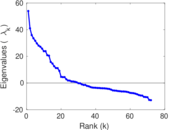
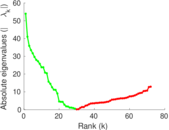
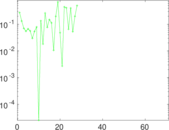
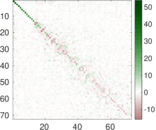
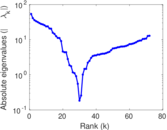
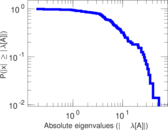
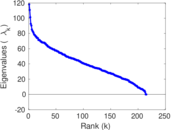
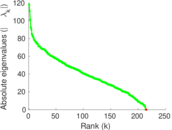
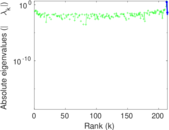
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Linton Clarke Freeman, Cynthia Marie Webster, and Deirdre M. Kirke.
Exploring social structure using dynamic three-dimensional color
images.
Soc. Netw., 20(2):109–118, 1998.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee




























































































































































