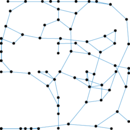
Gnutella (04)
This is a network of Gnutella hosts from 2002. The nodes represent Gnutella
hosts, and the directed edges represent connections between them. The dataset
is from August 04, 2002.
Metadata
Statistics
| Size | n = | 10,876
|
| Volume | m = | 39,994
|
| Loop count | l = | 0
|
| Wedge count | s = | 518,694
|
| Claw count | z = | 3,455,588
|
| Cross count | x = | 28,430,866
|
| Triangle count | t = | 934
|
| Square count | q = | 28,497
|
| 4-Tour count | T4 = | 2,382,740
|
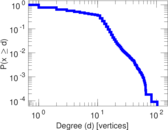
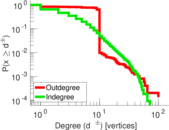
| Maximum degree | dmax = | 103
|
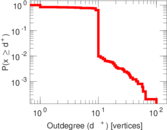
| Maximum outdegree | d+max = | 100
|
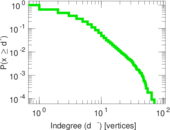
| Maximum indegree | d−max = | 72
|
| Average degree | d = | 7.354 54
|
| Fill | p = | 0.000 338 140
|
| Size of LCC | N = | 10,876
|
| Size of LSCC | Ns = | 4,317
|
| Relative size of LSCC | Nrs = | 0.396 929
|
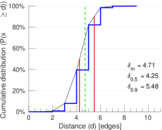
| Diameter | δ = | 10
|
| 50-Percentile effective diameter | δ0.5 = | 4.245 41
|
| 90-Percentile effective diameter | δ0.9 = | 5.476 31
|
| Median distance | δM = | 5
|
| Mean distance | δm = | 4.709 38
|
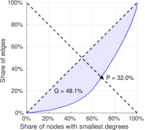
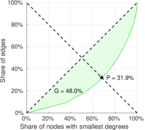
| Gini coefficient | G = | 0.480 592
|
| Balanced inequality ratio | P = | 0.319 510
|
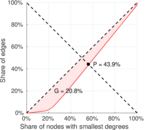
| Outdegree balanced inequality ratio | P+ = | 0.439 441
|
| Indegree balanced inequality ratio | P− = | 0.319 473
|
| Relative edge distribution entropy | Her = | 0.957 184
|
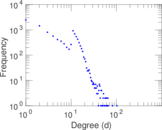
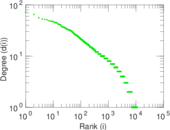
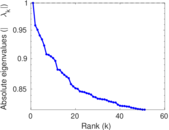
| Power law exponent | γ = | 1.668 00
|
| Tail power law exponent | γt = | 4.581 00
|
| Tail power law exponent with p | γ3 = | 4.581 00
|
| p-value | p = | 0.000 00
|
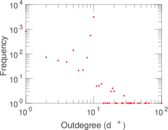
| Outdegree tail power law exponent with p | γ3,o = | 2.931 00
|
| Outdegree p-value | po = | 0.389 000
|
| Indegree tail power law exponent with p | γ3,i = | 3.401 00
|
| Indegree p-value | pi = | 0.601 000
|
| Degree assortativity | ρ = | −0.013 168 6
|
| Degree assortativity p-value | pρ = | 0.000 195 734
|
| In/outdegree correlation | ρ± = | +0.170 840
|
| Clustering coefficient | c = | 0.005 402 03
|
| Directed clustering coefficient | c± = | 0.004 999 17
|
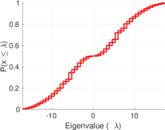
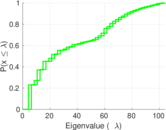
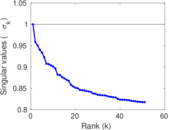
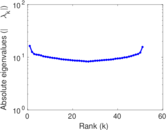
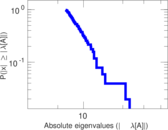
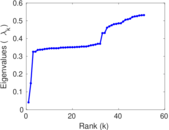
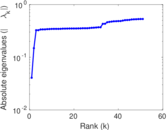
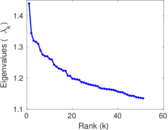
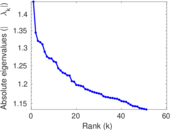
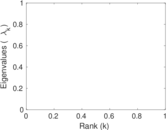
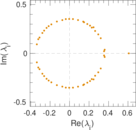
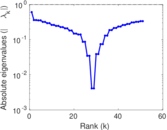
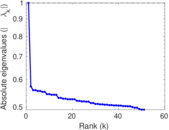
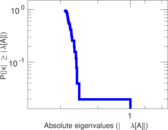
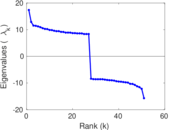
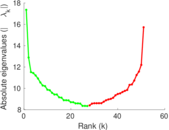
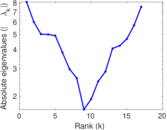
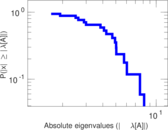
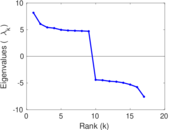
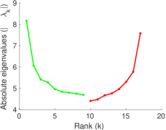
| Spectral norm | α = | 17.079 4
|
| Operator 2-norm | ν = | 15.413 4
|
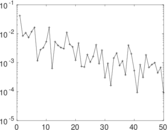
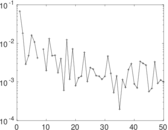
| Cyclic eigenvalue | π = | 4.446 96
|
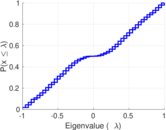
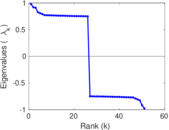
| Algebraic connectivity | a = | 0.040 828 2
|
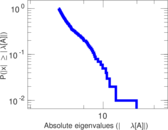
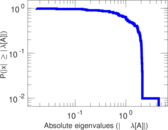
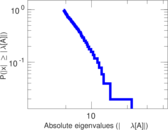
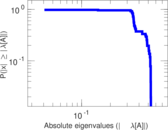
| Spectral separation | |λ1[A] / λ2[A]| = | 1.087 64
|
| Reciprocity | y = | 0.000 00
|
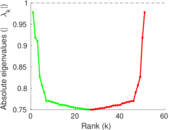
| Non-bipartivity | bA = | 0.080 574 4
|
| Normalized non-bipartivity | bN = | 0.021 890 1
|
| Algebraic non-bipartivity | χ = | 0.040 791 0
|
| Spectral bipartite frustration | bK = | 0.001 386 59
|
| Controllability | C = | 6,014
|
| Relative controllability | Cr = | 0.552 961
|
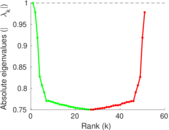
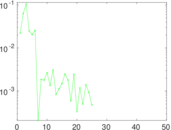
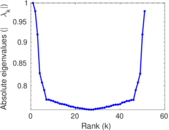
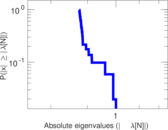
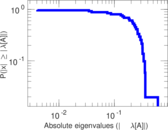
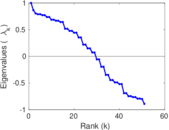
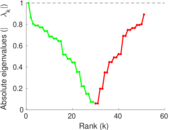
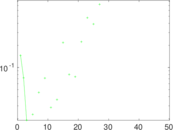
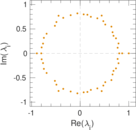
Plots


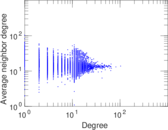
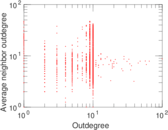
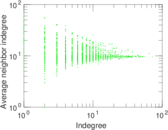
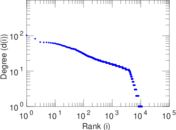
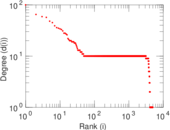




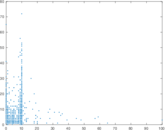
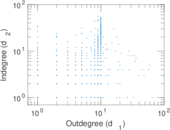
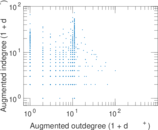
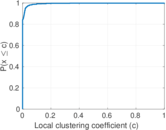
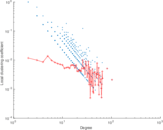
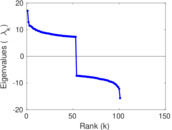
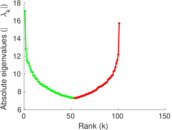
Matrix decompositions plots
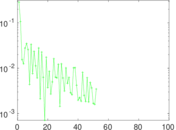
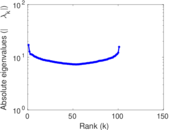
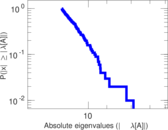
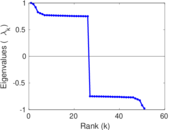
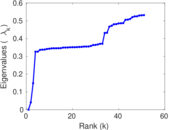
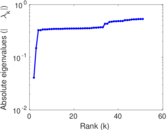
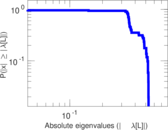
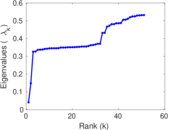
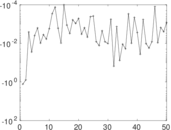
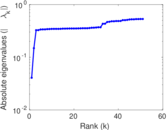
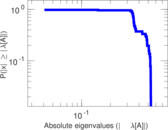
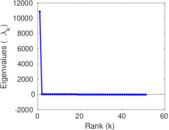
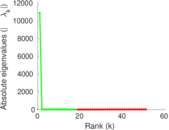
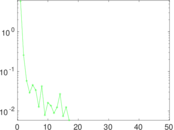
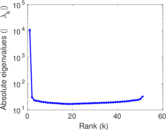
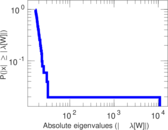
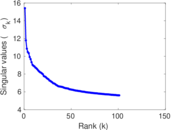
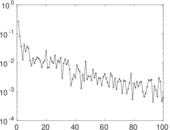
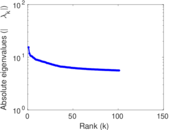
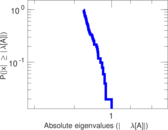
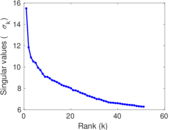
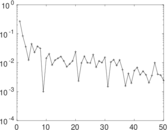
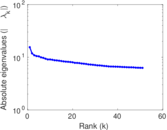
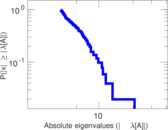
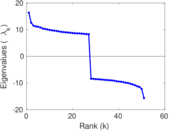
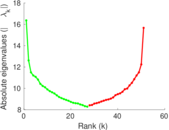
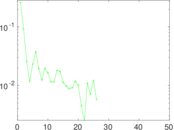
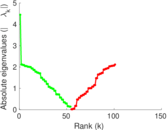
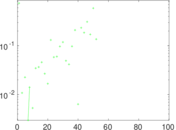
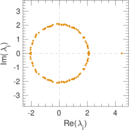
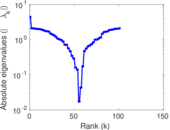
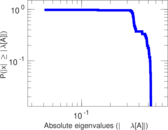
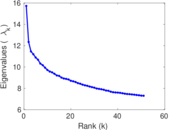
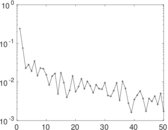
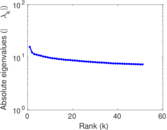
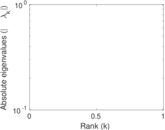
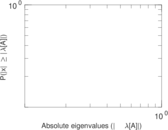
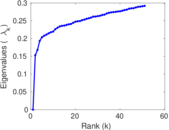
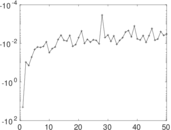
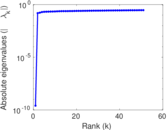
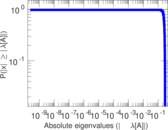
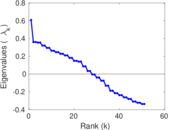
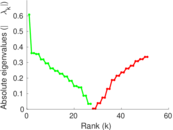
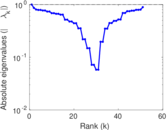
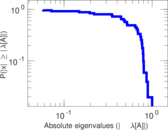
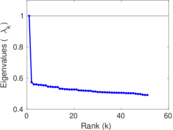
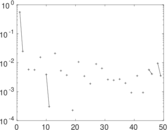
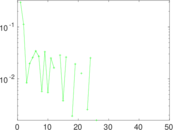
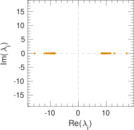
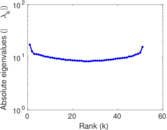
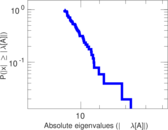
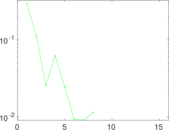
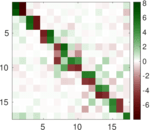
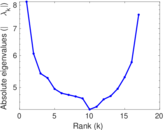
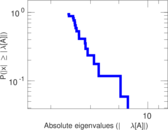
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Matei Ripeanu, Ian Foster, and Adriana Iamnitchi.
Mapping the Gnutella network: Properties of large-scale
peer-to-peer systems and implications for system design.
IEEE Internet Comput. J., 6, 2002.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee





















































































































































