Gnutella (30)
This is a network of Gnutella hosts from 2002. The nodes represent Gnutella
hosts, and the directed edges represent connections between them. The dataset
is from August 30, 2002.
Metadata
Statistics
| Size | n = | 36,682
|
| Volume | m = | 88,328
|
| Loop count | l = | 0
|
| Wedge count | s = | 923,756
|
| Claw count | z = | 4,477,812
|
| Cross count | x = | 19,735,194
|
| Triangle count | t = | 1,590
|
| Square count | q = | 46,363
|
| 4-Tour count | T4 = | 4,242,584
|
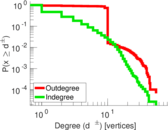
| Maximum degree | dmax = | 55
|
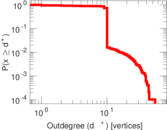
| Maximum outdegree | d+max = | 54
|
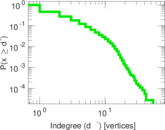
| Maximum indegree | d−max = | 54
|
| Average degree | d = | 4.815 88
|
| Fill | p = | 6.564 54 × 10−5
|
| Size of LCC | N = | 36,646
|
| Size of LSCC | Ns = | 8,490
|
| Relative size of LSCC | Nrs = | 0.231 449
|
| Diameter | δ = | 11
|
| 50-Percentile effective diameter | δ0.5 = | 5.456 36
|
| 90-Percentile effective diameter | δ0.9 = | 6.691 63
|
| Median distance | δM = | 6
|
| Mean distance | δm = | 5.898 38
|
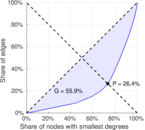
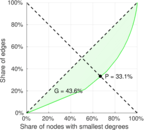
| Gini coefficient | G = | 0.558 875
|
| Balanced inequality ratio | P = | 0.264 050
|
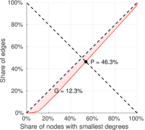
| Outdegree balanced inequality ratio | P+ = | 0.462 571
|
| Indegree balanced inequality ratio | P− = | 0.331 129
|
| Relative edge distribution entropy | Her = | 0.947 124
|
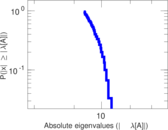
| Power law exponent | γ = | 2.035 68
|
| Tail power law exponent | γt = | 4.901 00
|
| Tail power law exponent with p | γ3 = | 4.901 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 4.331 00
|
| Outdegree p-value | po = | 0.012 000 0
|
| Indegree tail power law exponent with p | γ3,i = | 6.551 00
|
| Indegree p-value | pi = | 0.323 000
|
| Degree assortativity | ρ = | −0.103 375
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.303 441
|
| Clustering coefficient | c = | 0.005 163 70
|
| Directed clustering coefficient | c± = | 0.004 631 62
|
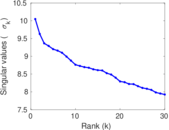
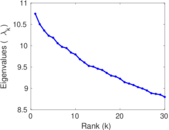
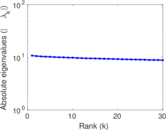
| Spectral norm | α = | 12.928 7
|
| Operator 2-norm | ν = | 9.985 77
|
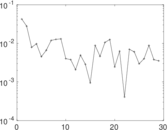
| Cyclic eigenvalue | π = | 3.874 98
|
| Algebraic connectivity | a = | 0.114 640
|
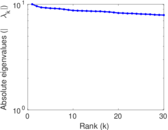
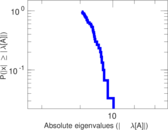
| Spectral separation | |λ1[A] / λ2[A]| = | 1.199 09
|
| Reciprocity | y = | 0.000 00
|
| Non-bipartivity | bA = | 0.166 035
|
| Normalized non-bipartivity | bN = | 0.061 233 1
|
| Algebraic non-bipartivity | χ = | 0.114 605
|
| Spectral bipartite frustration | bK = | 0.005 945 19
|
| Controllability | C = | 26,966
|
| Relative controllability | Cr = | 0.735 129
|
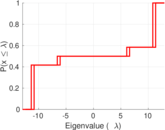
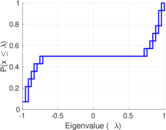
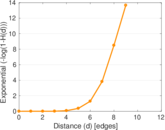
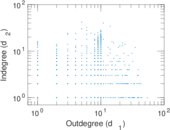
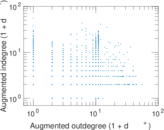
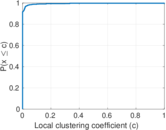
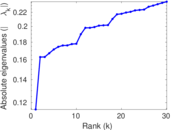
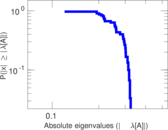
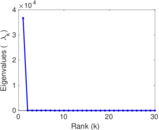
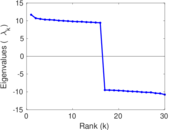
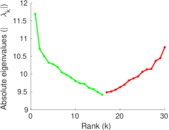
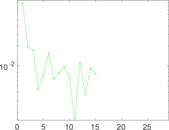
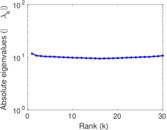
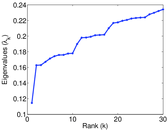
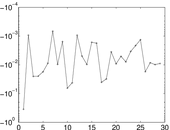
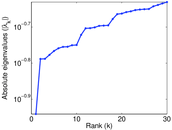
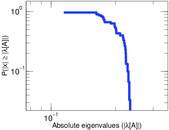
Plots

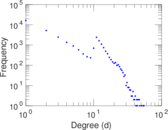
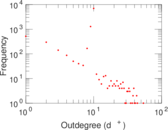
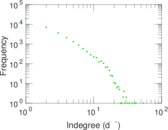
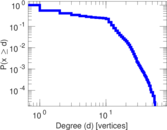
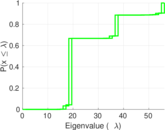
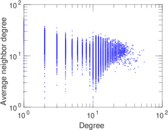
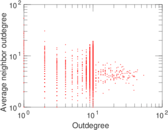
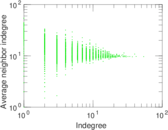
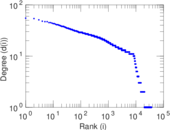
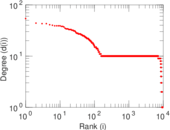
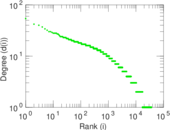
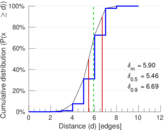
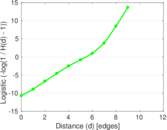
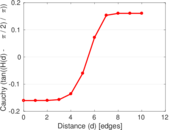
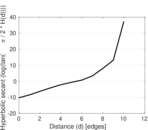
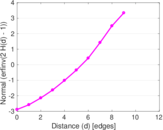
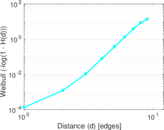






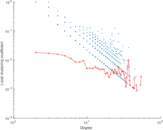
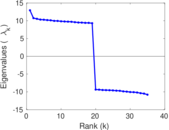
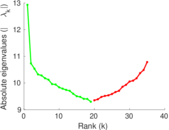
Matrix decompositions plots
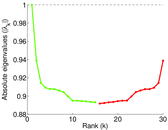
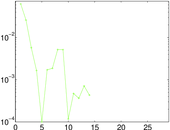
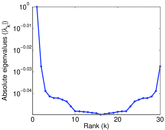
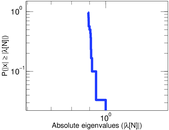
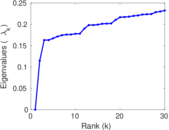
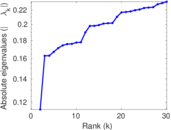
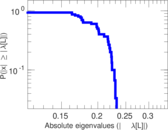

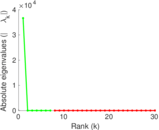
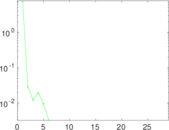
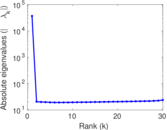
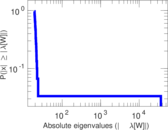
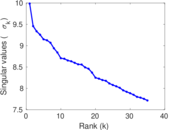
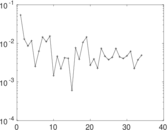
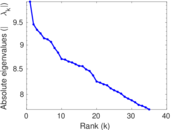
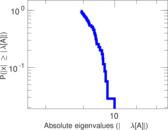
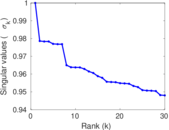
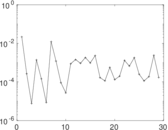
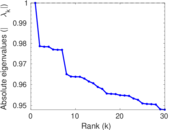
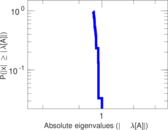
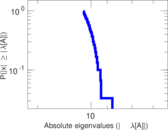
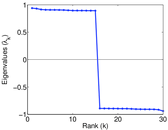
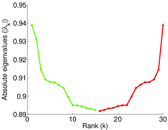
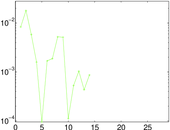
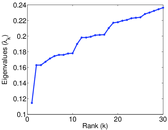
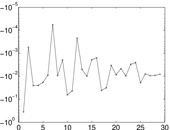
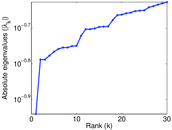
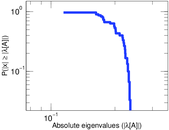
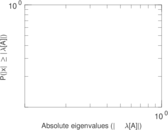
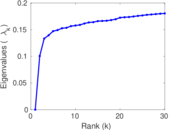
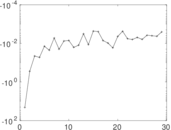
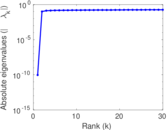
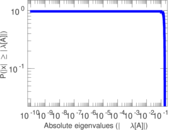
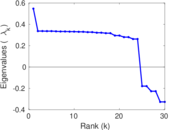
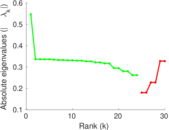
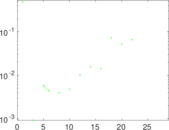
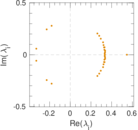
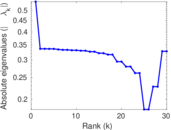
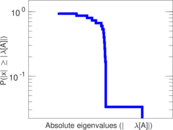
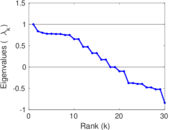
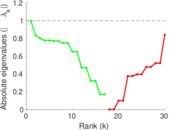
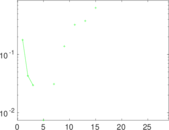
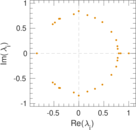
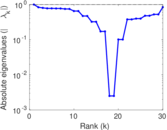
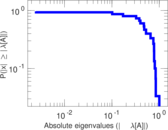
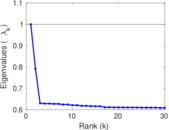
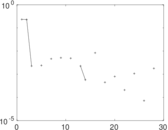
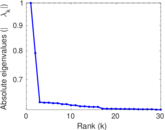
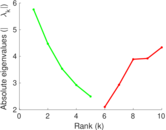
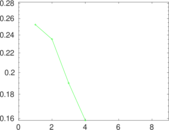
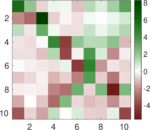
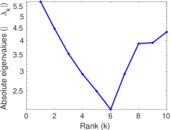
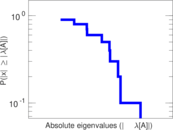
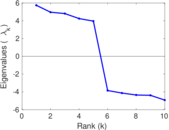
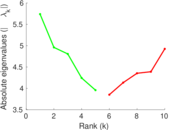
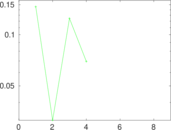
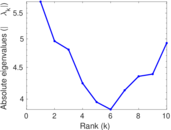
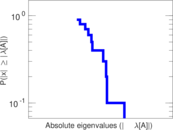
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Matei Ripeanu, Ian Foster, and Adriana Iamnitchi.
Mapping the Gnutella network: Properties of large-scale
peer-to-peer systems and implications for system design.
IEEE Internet Comput. J., 6, 2002.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee






















































































































































