Catster/Dogster
This Network contains familylinks between cats and cats, cats and dogs, as well
as dogs and dogs from the social websites catster.com and dogster.com. Also
included are cat-cat and dog-dog friendships.
Metadata
Statistics
| Size | n = | 623,766
|
| Volume | m = | 15,699,276
|
| Loop count | l = | 4,110
|
| Wedge count | s = | 69,385,263,164
|
| Claw count | z = | 1,209,782,326,650,986
|
| Cross count | x = | 2.142 41 × 1019
|
| Triangle count | t = | 656,390,451
|
| Square count | q = | 770,091,837,319
|
| 4-Tour count | T4 = | 6,438,307,141,540
|
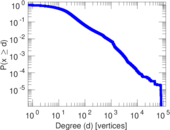
| Maximum degree | dmax = | 80,637
|
| Average degree | d = | 50.337 1
|
| Fill | p = | 8.069 85 × 10−5
|
| Size of LCC | N = | 601,213
|
| Diameter | δ = | 15
|
| 50-Percentile effective diameter | δ0.5 = | 3.510 76
|
| 90-Percentile effective diameter | δ0.9 = | 5.207 71
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 4.101 62
|
| Gini coefficient | G = | 0.767 780
|
| Balanced inequality ratio | P = | 0.203 553
|
| Relative edge distribution entropy | Her = | 0.860 330
|
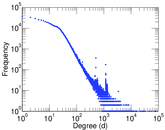
| Power law exponent | γ = | 1.378 63
|
| Tail power law exponent | γt = | 2.131 00
|
| Degree assortativity | ρ = | −0.085 620 5
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| Clustering coefficient | c = | 0.028 380 3
|
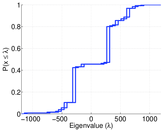
| Spectral norm | α = | 1,190.93
|
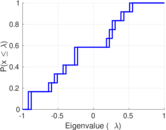
| Algebraic connectivity | a = | 0.000 850 501
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.000 30
|
| Non-bipartivity | bA = | 0.147 442
|
| Normalized non-bipartivity | bN = | 0.071 405 9
|
| Controllability | C = | 74,397
|
Plots
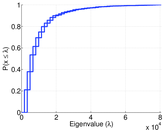
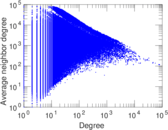
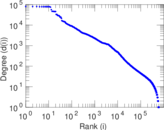
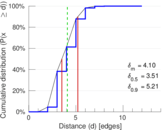
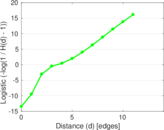
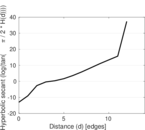
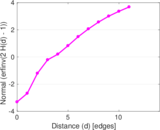
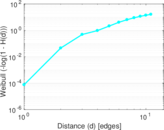
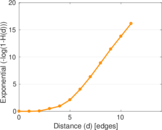
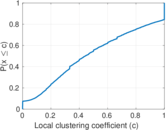
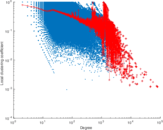
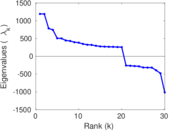
Matrix decompositions plots
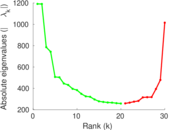
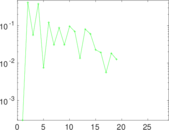
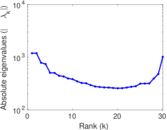
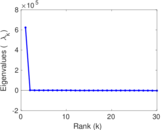
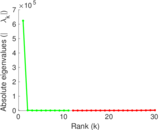
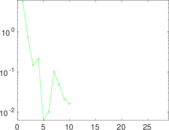
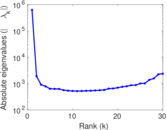
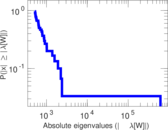
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
KONECT ‣ Networks ‣
Buy Me a Coffee
