Hamsterster households

Metadata

Code		`PHh`
Internal name		`petster-hamster-household`
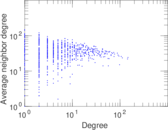
Name		Hamsterster households
Availability		Dataset is available for download
Consistency check		Dataset passed all tests
Category		Online social network
Network format		Unipartite, undirected
Edge type		Unweighted, no multiple edges
Loops		Does not contain loops

Size	n =	1,576
Volume	m =	4,032
Loop count	l =	0
Wedge count	s =	132,815
Claw count	z =	3,056,139
Cross count	x =	72,660,046
Triangle count	t =	5,811
Square count	q =	113,083
4-Tour count	T₄ =	1,443,988
Maximum degree	d_max =	147
Average degree	d =	5.116 75
Fill	p =	0.009 517 07
Size of LCC	N =	874
Diameter	δ =	8
50-Percentile effective diameter	δ_0.5 =	2.610 53
90-Percentile effective diameter	δ_0.9 =	3.885 03
Median distance	δ_M =	3
Mean distance	δ_m =	3.174 29
Gini coefficient	G =	0.630 196
Balanced inequality ratio	P =	0.257 812
Relative edge distribution entropy	H_er =	0.887 146
Power law exponent	γ =	1.707 77
Tail power law exponent	γ_t =	2.141 00
Tail power law exponent with p	γ₃ =	2.141 00
p-value	p =	0.002 000 00
Degree assortativity	ρ =	−0.120 689
Degree assortativity p-value	p_ρ =	1.500 97 × 10⁻²⁷
Clustering coefficient	c =	0.131 258
Spectral norm	α =	31.972 7
Algebraic connectivity	a =	0.213 281
Spectral separation	\|λ₁[A] / λ₂[A]\| =	2.066 50
Non-bipartivity	b_A =	0.565 705
Normalized non-bipartivity	b_N =	0.119 673
Algebraic non-bipartivity	χ =	0.212 564
Spectral bipartite frustration	b_K =	0.005 801 31
Controllability	C =	215
Relative controllability	C_r =	0.233 442