Euroroads

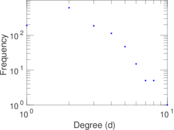
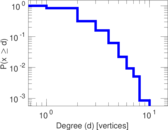
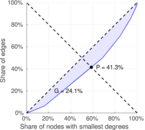
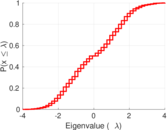
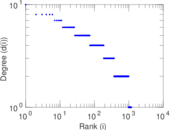
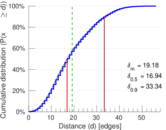
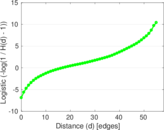
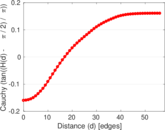
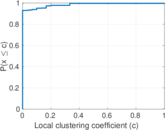
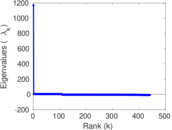
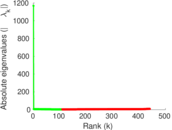
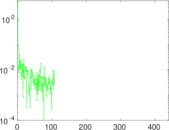
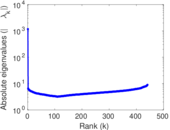
This is the international E-road network, a road network located mostly in Europe. The network is undirected; nodes represent cities and an edge between two nodes denotes that they are connected by an E-road.

Metadata

Code		`ET`
Internal name		`subelj_euroroad`
Name		Euroroads
Data source		http://lovro.lpt.fri.uni-lj.si/support.jsp
Availability		Dataset is available for download
Consistency check		Dataset passed all tests
Category		Infrastructure network
Node meaning		City
Edge meaning		Road
Network format		Unipartite, undirected
Edge type		Unweighted, no multiple edges
Loops		Does not contain loops

Statistics

Size	n =	1,174
Volume	m =	1,417
Loop count	l =	0
Wedge count	s =	2,833
Claw count	z =	1,983
Cross count	x =	1,308
Triangle count	t =	32
Square count	q =	41
4-Tour count	T₄ =	14,494
Maximum degree	d_max =	10
Average degree	d =	2.413 97
Fill	p =	0.002 057 94
Size of LCC	N =	1,039
Diameter	δ =	62
50-Percentile effective diameter	δ_0.5 =	16.935 8
90-Percentile effective diameter	δ_0.9 =	33.340 5
Median distance	δ_M =	17
Mean distance	δ_m =	19.181 2
Gini coefficient	G =	0.240 881
Balanced inequality ratio	P =	0.412 844
Relative edge distribution entropy	H_er =	0.984 809
Power law exponent	γ =	2.289 90
Tail power law exponent	γ_t =	6.401 00
Tail power law exponent with p	γ₃ =	6.401 00
p-value	p =	0.713 000
Degree assortativity	ρ =	+0.126 684
Degree assortativity p-value	p_ρ =	1.302 58 × 10⁻¹¹
Clustering coefficient	c =	0.033 886 3
Spectral norm	α =	4.010 44
Algebraic connectivity	a =	0.001 160 30
Spectral separation	\|λ₁[A] / λ₂[A]\| =	1.023 07
Non-bipartivity	b_A =	0.061 239 9
Normalized non-bipartivity	b_N =	0.004 177 77
Algebraic non-bipartivity	χ =	0.008 094 25
Spectral bipartite frustration	b_K =	0.000 805 549
Controllability	C =	103
Relative controllability	C_r =	0.087 734 2

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Clustering coefficient distribution

Average neighbor degree distribution

SynGraphy

Matrix decompositions plots

Downloads

References

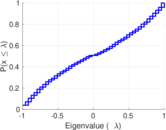
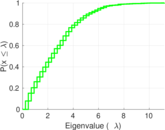
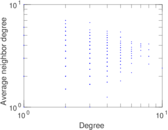
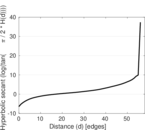
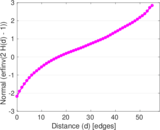
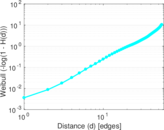
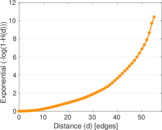
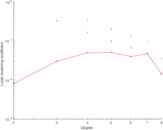
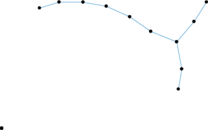
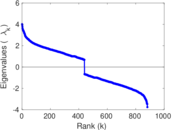
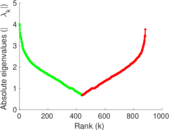
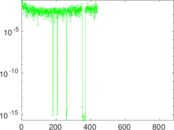
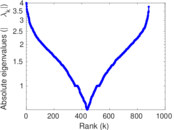
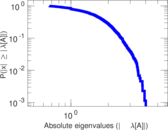
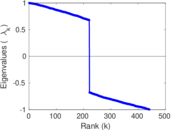
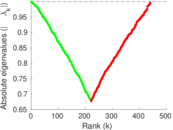
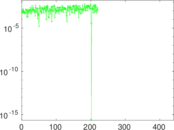
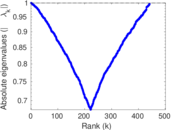
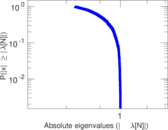
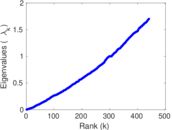
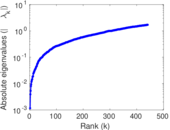
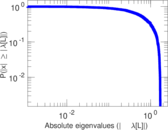
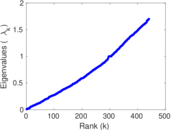
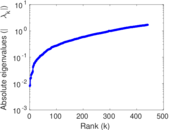
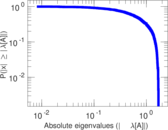
[1]	Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2]	Lovro Šubelj and Marko Bajec. Robust network community detection using balanced propagation. Eur. Phys. J. B, 81(3):353–362, 2011.