JUNG/Javax
This is the software class dependency network of the JUNG 2.0.1 and javax
1.6.0.7 libraries, namespaces edu.uci.ics.jung and java/javax. The network is
directed. Nodes represent classes. An edge between them indicates that there
exists a dependency between two classes. As there may be multiple references
between classes the network has multiple edges.
Metadata
Statistics
| Size | n = | 6,120
|
| Volume | m = | 138,706
|
| Unique edge count | m̿ = | 50,535
|
| Loop count | l = | 0
|
| Wedge count | s = | 49,825,722
|
| Claw count | z = | 85,378,501,686
|
| Cross count | x = | 117,750,526,945,905
|
| Triangle count | t = | 182,139
|
| Square count | q = | 80,032,387
|
| 4-Tour count | T4 = | 839,662,564
|
| Maximum degree | dmax = | 26,133
|
| Maximum outdegree | d+max = | 375
|
| Maximum indegree | d−max = | 26,110
|
| Average degree | d = | 45.328 8
|
| Fill | p = | 0.001 349 46
|
| Average edge multiplicity | m̃ = | 2.744 75
|
| Size of LCC | N = | 6,120
|
| Size of LSCC | Ns = | 77
|
| Relative size of LSCC | Nrs = | 0.012 581 7
|
| Diameter | δ = | 7
|
| 50-Percentile effective diameter | δ0.5 = | 1.534 08
|
| 90-Percentile effective diameter | δ0.9 = | 1.963 50
|
| Median distance | δM = | 2
|
| Mean distance | δm = | 2.064 48
|
| Gini coefficient | G = | 0.752 594
|
| Balanced inequality ratio | P = | 0.204 468
|
| Outdegree balanced inequality ratio | P+ = | 0.263 702
|
| Indegree balanced inequality ratio | P− = | 0.100 421
|
| Relative edge distribution entropy | Her = | 0.825 325
|
| Power law exponent | γ = | 1.487 25
|
| Tail power law exponent | γt = | 2.341 00
|
| Tail power law exponent with p | γ3 = | 2.341 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 2.821 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 1.781 00
|
| Indegree p-value | pi = | 0.026 000 0
|
| Degree assortativity | ρ = | −0.232 705
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | −0.005 123 21
|
| Clustering coefficient | c = | 0.010 966 6
|
| Directed clustering coefficient | c± = | 0.450 877
|
| Spectral norm | α = | 913.941
|
| Operator 2-norm | ν = | 893.925
|
| Cyclic eigenvalue | π = | 16.877 2
|
| Algebraic connectivity | a = | 0.401 225
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.044 74
|
| Reciprocity | y = | 0.009 696 25
|
| Non-bipartivity | bA = | 0.042 822 8
|
| Normalized non-bipartivity | bN = | 0.162 291
|
| Algebraic non-bipartivity | χ = | 0.319 511
|
| Spectral bipartite frustration | bK = | 0.004 860 33
|
| Controllability | C = | 4,057
|
| Relative controllability | Cr = | 0.662 908
|
Plots

















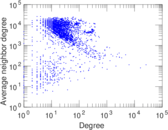

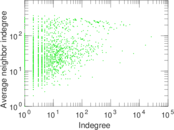























Matrix decompositions plots















































































































Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Lovro Šubelj and Marko Bajec.
Software systems through complex networks science: Review, analysis
and applications.
In Proc. Int. Workshop on Software Min., pages 9–16, 2012.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee

























































































































































