Stack Overflow

These are interactions from the StackExchange site "Stack Overflow". The network is between users, and directed edges represent three types of interactions: answering a question of another user, commenting on another user's question, and commenting on another user's answer. The network is temporal. This network is part of a series of network from multiple StackExchange sites.

Metadata

Codest
Internal namesx-stackoverflow
NameStack Overflow
Data sourcehttp://snap.stanford.edu/data/sx-Stack
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Online contact network
Node meaningUser
Edge meaningAnswer/comment
Network formatUnipartite, directed
Edge typeUnweighted, multiple edges
Temporal data Edges are annotated with timestamps
ReciprocalContains reciprocal edges
Directed cyclesContains directed cycles
LoopsContains loops
Snapshot Is a snapshot and likely to not contain all data

Statistics

Size n =2,601,977
Volume m =63,497,050
Unique edge count m̿ =36,233,450
Loop count l =15,593,784
Wedge count s =32,544,604,487
Claw count z =233,017,508,108,735
Cross count x =1,726,160,310,355,354,368
Triangle count t =114,206,974
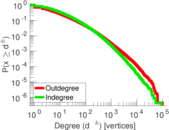
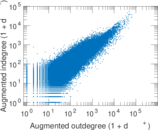
Maximum degree dmax =194,806
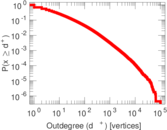
Maximum outdegree d+max =101,663
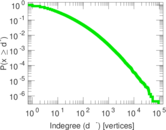
Maximum indegree d−max =93,143
Average degree d =48.806 8
Fill p =5.351 84 × 10−6
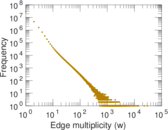
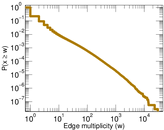
Average edge multiplicity m̃ =1.752 44
Size of LCC N =2,572,345
Size of LSCC Ns =1,642,130
Relative size of LSCC Nrs =0.631 109
Diameter δ =11
50-Percentile effective diameter δ0.5 =3.415 07
90-Percentile effective diameter δ0.9 =4.413 11
Median distance δM =4
Mean distance δm =3.912 38
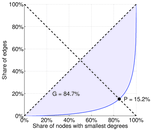
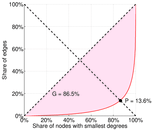
Gini coefficient G =0.847 135
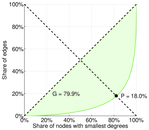
Balanced inequality ratio P =0.151 529
Outdegree balanced inequality ratio P+ =0.136 489
Indegree balanced inequality ratio P− =0.179 913
Relative edge distribution entropy Her =0.868 730
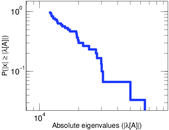
Power law exponent γ =1.617 00
Tail power law exponent γt =1.951 00
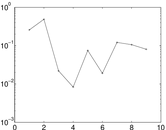
Degree assortativity ρ =−0.066 374 2
Degree assortativity p-value pρ =0.000 00
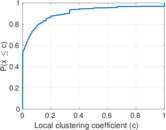
Clustering coefficient c =0.010 527 7
Directed clustering coefficient c± =0.010 757 2
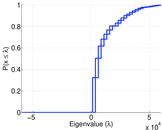
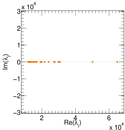
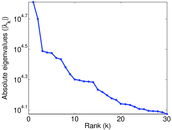
Spectral norm α =59,877.4
Operator 2-norm ν =29,943.5
Cyclic eigenvalue π =29,933.2
Reciprocity y =0.406 864
Non-bipartivity bA =0.998 689
Normalized non-bipartivity bN =0.050 881 6
Algebraic non-bipartivity χ =0.087 859 8
Spectral bipartite frustration bK =0.000 957 115

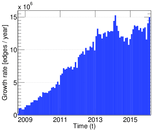
Plots

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the normalized adjacency matrix

Hop distribution

In/outdegree scatter plot

Edge weight/multiplicity distribution

Clustering coefficient distribution

Temporal distribution

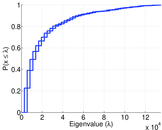
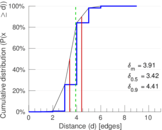
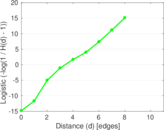
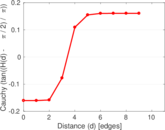
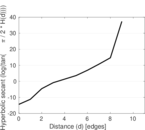
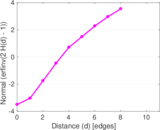
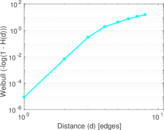
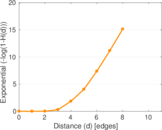
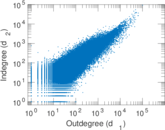
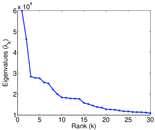
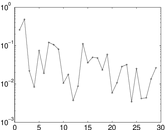
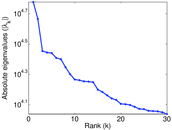
Matrix decompositions plots

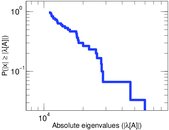
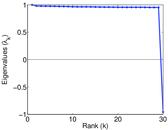
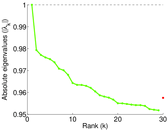
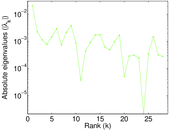
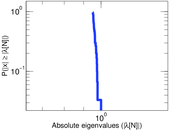
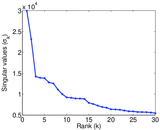
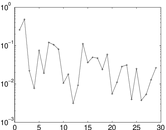
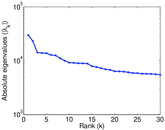
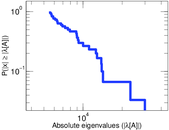
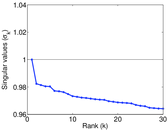
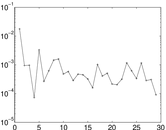
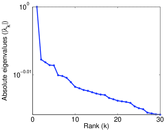
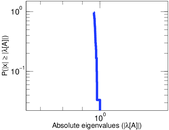
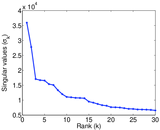
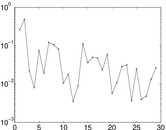
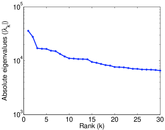
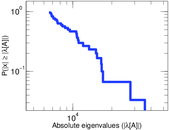
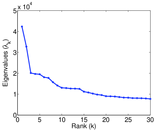
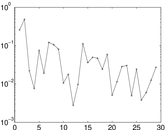
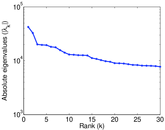
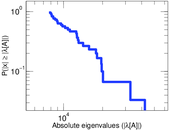
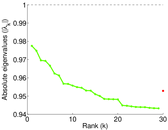
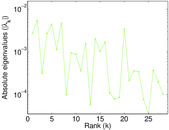
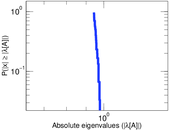
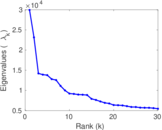
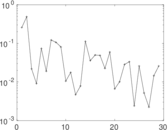
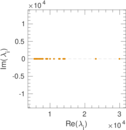
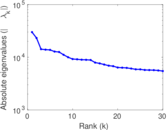
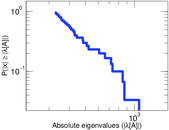
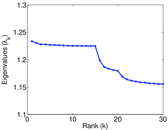
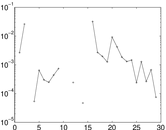
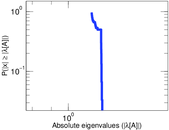
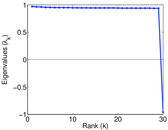
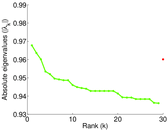
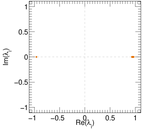
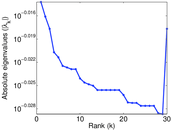
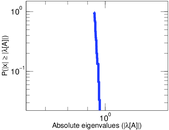
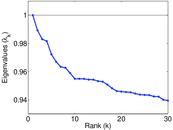
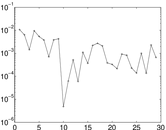
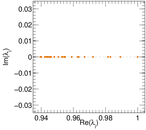
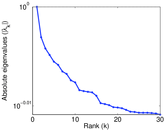
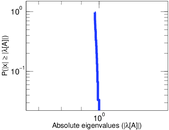
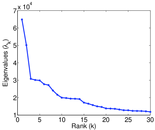
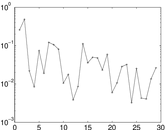
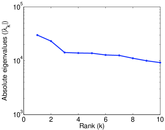
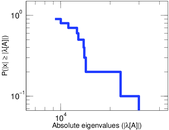
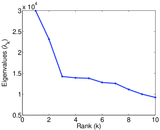
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Jure Leskovec. Stanford Network Analysis Project. http://snap.stanford.edu/, September 2014.