Notre Dame
This is the directed network of hyperlinks between the web pages from the
website of the University of Notre Dame.
Metadata
Statistics
| Size | n = | 325,729
|
| Volume | m = | 1,497,134
|
| Wedge count | s = | 304,881,174
|
| Claw count | z = | 469,365,457,284
|
| Cross count | x = | 887,074,893,174,903
|
| Triangle count | t = | 8,910,005
|
| Square count | q = | 884,960,527
|
| 4-Tour count | T4 = | 8,301,389,128
|
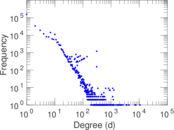
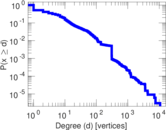
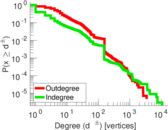
| Maximum degree | dmax = | 10,721
|
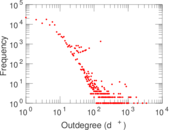
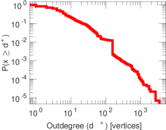
| Maximum outdegree | d+max = | 3,445
|
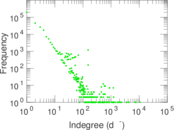
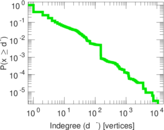
| Maximum indegree | d−max = | 10,721
|
| Average degree | d = | 9.192 51
|
| Fill | p = | 1.411 07 × 10−5
|
| Size of LCC | N = | 325,729
|
| Diameter | δ = | 46
|
| 50-Percentile effective diameter | δ0.5 = | 6.259 30
|
| 90-Percentile effective diameter | δ0.9 = | 8.915 59
|
| Median distance | δM = | 7
|
| Mean distance | δm = | 6.956 28
|
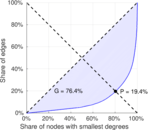
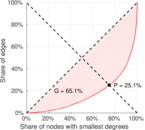
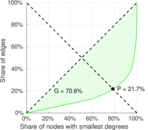
| Gini coefficient | G = | 0.764 078
|
| Balanced inequality ratio | P = | 0.194 482
|
| Outdegree balanced inequality ratio | P+ = | 0.251 254
|
| Indegree balanced inequality ratio | P− = | 0.217 295
|
| Relative edge distribution entropy | Her = | 0.875 892
|
| Power law exponent | γ = | 2.107 22
|
| Tail power law exponent | γt = | 2.151 00
|
| Tail power law exponent with p | γ3 = | 2.151 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 2.131 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 1.991 00
|
| Indegree p-value | pi = | 0.000 00
|
| Degree assortativity | ρ = | −0.053 440 7
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.710 200
|
| Clustering coefficient | c = | 0.087 673 6
|
| Directed clustering coefficient | c± = | 0.713 487
|
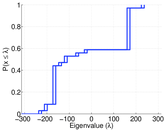
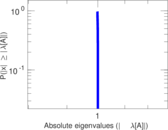
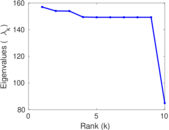
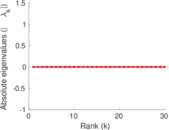
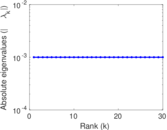
| Spectral norm | α = | 314.060
|
| Operator 2-norm | ν = | 170.642
|
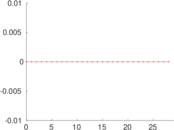
| Algebraic connectivity | a = | 0.000 190 992
|
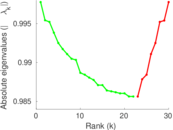
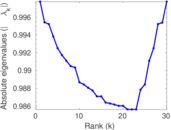
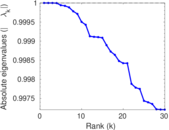
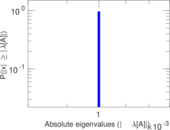
| Spectral separation | |λ1[A] / λ2[A]| = | 1.019 73
|
| Reciprocity | y = | 0.525 402
|
| Non-bipartivity | bA = | 0.667 646
|
| Normalized non-bipartivity | bN = | 4.997 07 × 10−5
|
| Spectral bipartite frustration | bK = | 4.040 25 × 10−6
|
| Controllability | C = | 222,148
|
| Relative controllability | Cr = | 0.682 003
|
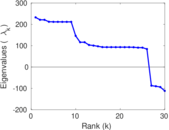
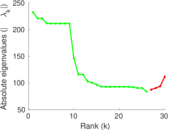
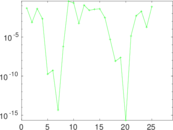
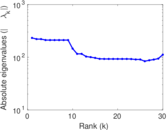
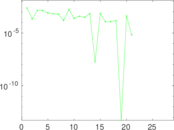
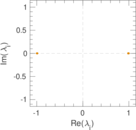
Plots

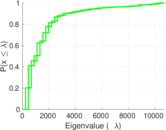


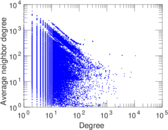
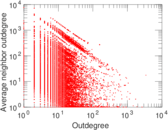
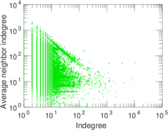
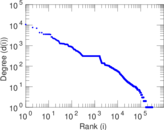
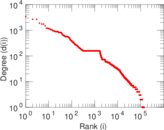
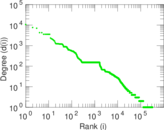

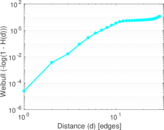
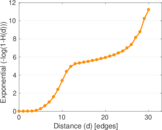
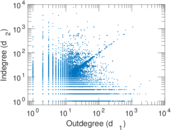
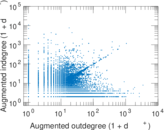
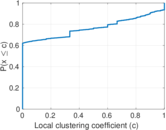
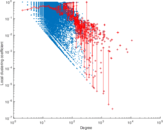
Matrix decompositions plots
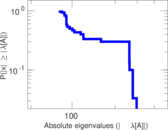
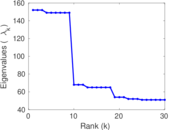
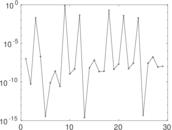
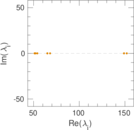
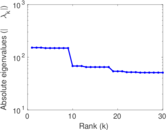
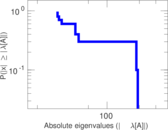
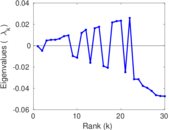
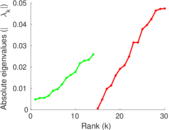
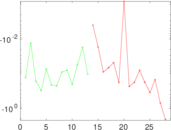
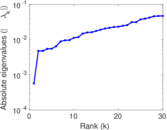
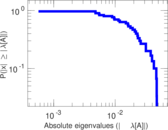
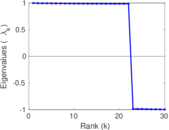
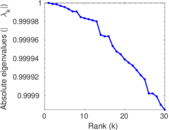
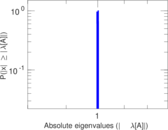
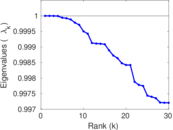
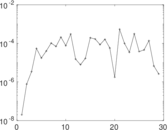
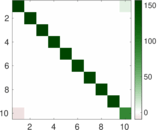
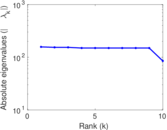
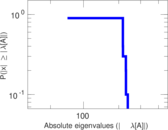
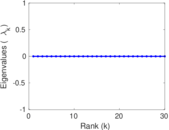
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Réka Albert, Hawoong Jeong, and Albert-Laszlo Barabási.
Internet: Diameter of the world wide web.
Nature, 401(6749):130–131, Sep 1999.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee















































































