Stanford

This is the directed network of hyperlinks between the web pages from the website of the Stanford University.

Metadata

CodeSF
Internal nameweb-Stanford
NameStanford
Data sourcehttp://snap.stanford.edu/data/web-Stanford.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Hyperlink network
Dataset timestamp 2002
Node meaningWebpage
Edge meaningHyperlink
Network formatUnipartite, directed
Edge typeUnweighted, no multiple edges
ReciprocalContains reciprocal edges
Directed cyclesContains directed cycles
LoopsDoes not contain loops

Statistics

Size n =281,903
Volume m =2,312,497
Wedge count s =3,944,069,093
Claw count z =25,253,733,860,230
Triangle count t =11,329,473
Square count q =13,316,840,570
4-Tour count T4 =122,314,986,204
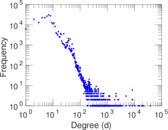
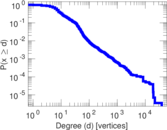
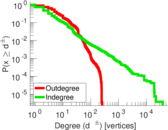
Maximum degree dmax =38,626
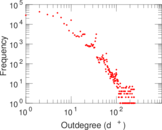
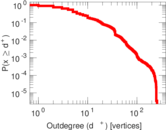
Maximum outdegree d+max =255
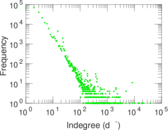
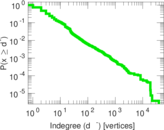
Maximum indegree d−max =38,606
Average degree d =16.406 3
Fill p =2.909 94 × 10−5
Size of LCC N =255,265
Size of LSCC Ns =150,532
Relative size of LSCC Nrs =0.533 985
Diameter δ =164
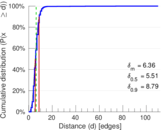
50-Percentile effective diameter δ0.5 =5.507 63
90-Percentile effective diameter δ0.9 =8.788 03
Median distance δM =6
Mean distance δm =6.362 93
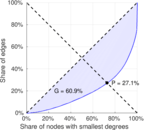
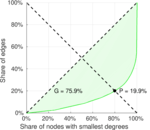
Gini coefficient G =0.609 279
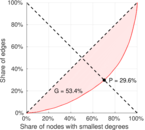
Balanced inequality ratio P =0.270 840
Outdegree balanced inequality ratio P+ =0.296 020
Indegree balanced inequality ratio P− =0.199 346
Relative edge distribution entropy Her =0.894 113
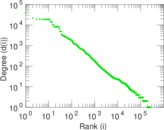
Power law exponent γ =1.537 77
Degree assortativity ρ =−0.112 445
Degree assortativity p-value pρ =0.000 00
In/outdegree correlation ρ± =+0.329 225
Clustering coefficient c =0.008 617 60
Directed clustering coefficient c± =0.430 381
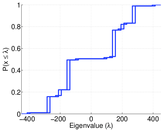
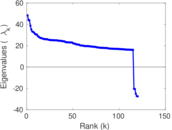
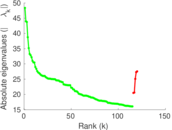
Spectral norm α =449.572
Operator 2-norm ν =438.345
Algebraic connectivity a =0.000 171 694
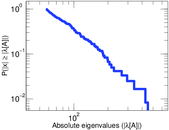
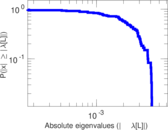
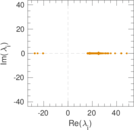
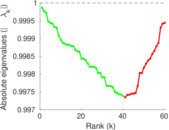
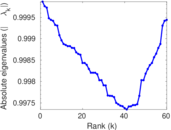
Spectral separation |λ1[A] / λ2[A]| =1.051 30
Reciprocity y =0.276 637
Non-bipartivity bA =0.048 796 6
Normalized non-bipartivity bN =0.000 583 688
Spectral bipartite frustration bK =2.329 34 × 10−5
Controllability C =97,500
Relative controllability Cr =0.345 864

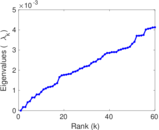
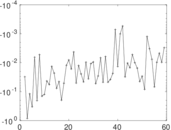
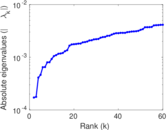
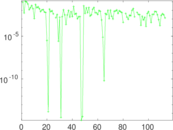
Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Delaunay graph drawing

In/outdegree scatter plot

Clustering coefficient distribution

SynGraphy

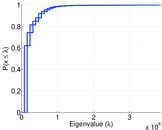
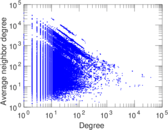
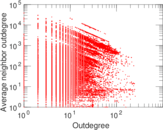
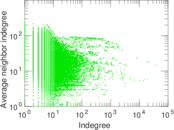
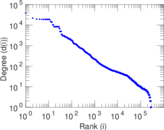
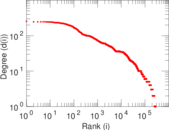
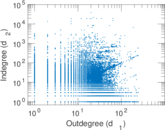
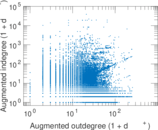
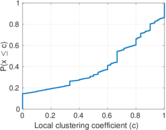
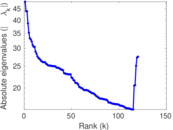
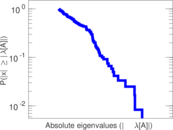
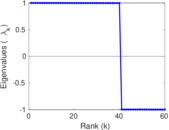
Matrix decompositions plots

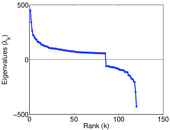
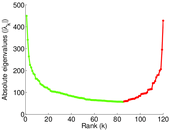
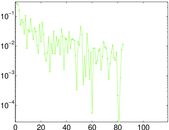
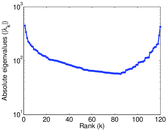
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Jure Leskovec, Kevin Lang, Anirban Dasgupta, and Michael W. Mahoney. Community structure in large networks: Natural cluster sizes and the absence of large well-defined clusters. Internet Math., 6(1):29–123, 2009.