Wikipedia links (fiu-vro)
This network consists of the wikilinks of the Wikipedia in the Võro language
(fiu-vro). Nodes are Wikipedia articles, and directed edges are wikilinks,
i.e., hyperlinks within one wiki. In the wiki source, these are indicated with
[[double brackets]]. Only pages in the article namespace are included.
Metadata
Statistics
| Size | n = | 6,424
|
| Volume | m = | 280,614
|
| Loop count | l = | 2
|
| Wedge count | s = | 45,396,041
|
| Claw count | z = | 37,328,723,112
|
| Cross count | x = | 7,339,763,364,382
|
| Triangle count | t = | 13,036,980
|
| Square count | q = | 3,345,511,441
|
| 4-Tour count | T4 = | 26,945,988,978
|
| Maximum degree | dmax = | 2,191
|
| Maximum outdegree | d+max = | 437
|
| Maximum indegree | d−max = | 2,151
|
| Average degree | d = | 87.364 3
|
| Fill | p = | 0.006 799 83
|
| Size of LCC | N = | 6,401
|
| Size of LSCC | Ns = | 4,817
|
| Relative size of LSCC | Nrs = | 0.749 844
|
| Diameter | δ = | 10
|
| 50-Percentile effective diameter | δ0.5 = | 2.876 72
|
| 90-Percentile effective diameter | δ0.9 = | 4.037 52
|
| Median distance | δM = | 3
|
| Mean distance | δm = | 3.400 46
|
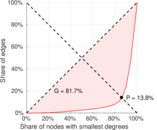
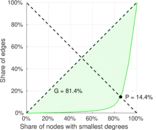
| Gini coefficient | G = | 0.829 219
|
| Balanced inequality ratio | P = | 0.126 676
|
| Outdegree balanced inequality ratio | P+ = | 0.138 019
|
| Indegree balanced inequality ratio | P− = | 0.144 137
|
| Relative edge distribution entropy | Her = | 0.824 193
|
| Power law exponent | γ = | 1.446 95
|
| Tail power law exponent | γt = | 1.651 00
|
| Tail power law exponent with p | γ3 = | 1.651 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 1.621 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 1.421 00
|
| Indegree p-value | pi = | 0.000 00
|
| Degree assortativity | ρ = | +0.198 302
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.883 943
|
| Clustering coefficient | c = | 0.861 550
|
| Directed clustering coefficient | c± = | 0.970 614
|
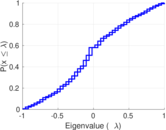
| Spectral norm | α = | 760.305
|
| Operator 2-norm | ν = | 382.220
|
| Cyclic eigenvalue | π = | 378.068
|
| Algebraic connectivity | a = | 0.135 780
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.496 64
|
| Reciprocity | y = | 0.883 562
|
| Non-bipartivity | bA = | 0.937 193
|
| Normalized non-bipartivity | bN = | 0.064 840 6
|
| Algebraic non-bipartivity | χ = | 0.122 408
|
| Spectral bipartite frustration | bK = | 0.000 625 308
|
| Controllability | C = | 2,580
|
| Relative controllability | Cr = | 0.401 619
|
Plots

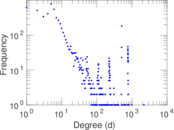
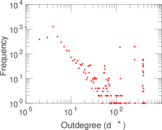
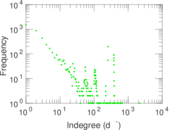
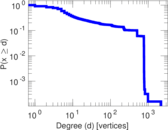
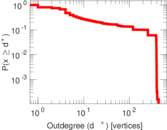
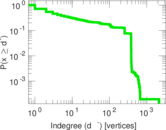
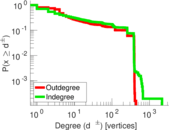
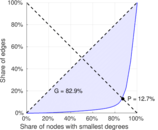



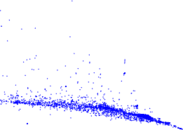
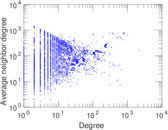
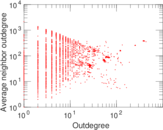
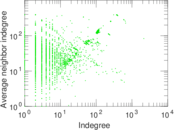
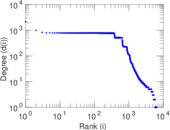
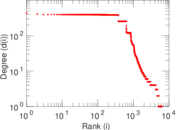
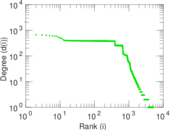



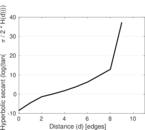
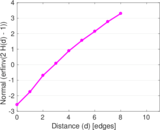
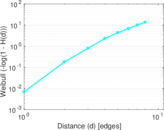
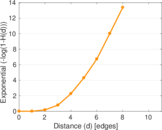





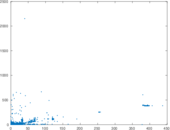
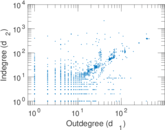
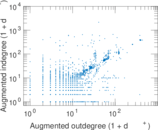
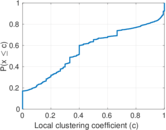
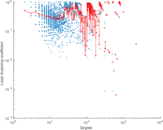

Matrix decompositions plots
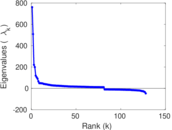
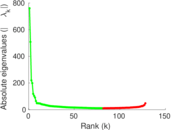
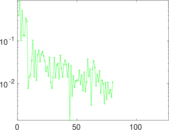
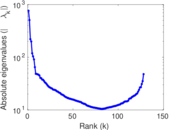
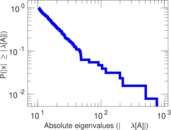
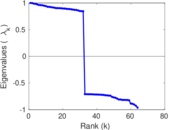
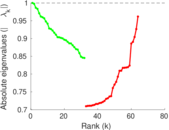
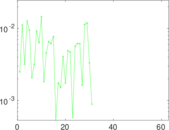
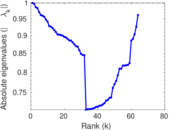
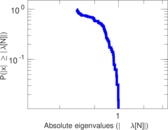
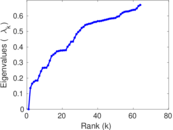
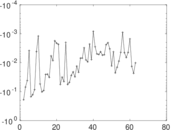
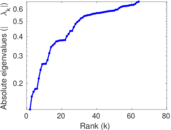
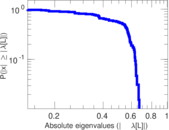
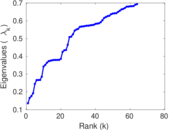
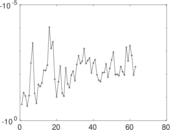
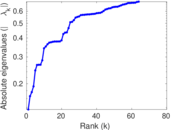
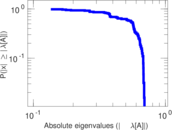
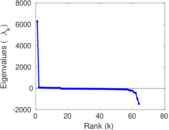
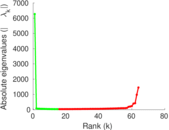
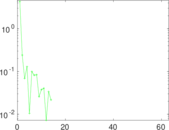
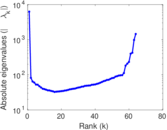
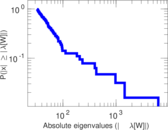
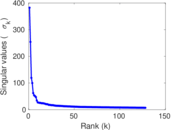
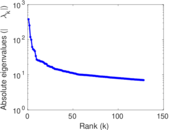
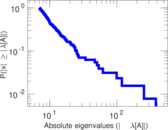
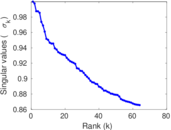
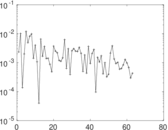
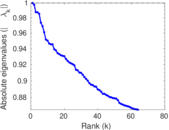
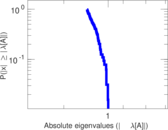
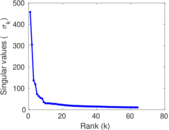
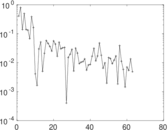
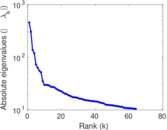
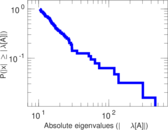
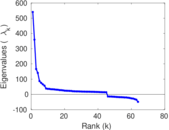
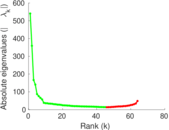
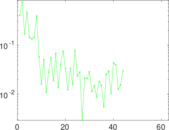
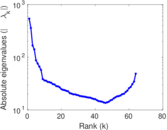
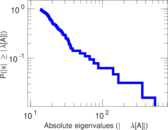
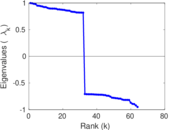
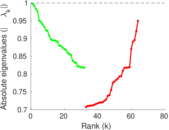
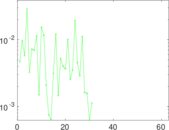
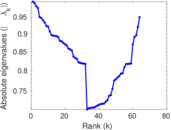
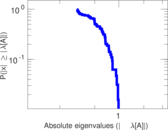
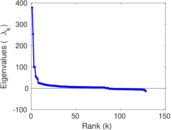
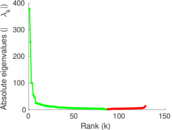
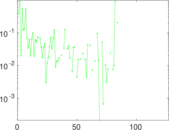
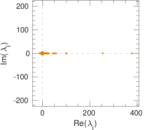
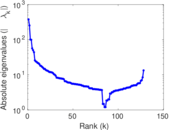
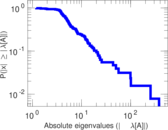
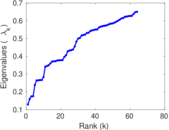
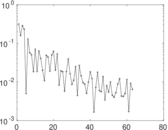
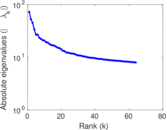
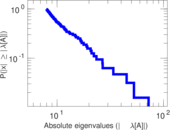
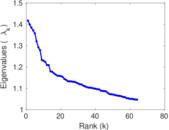
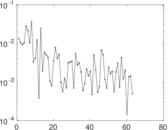
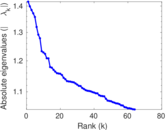
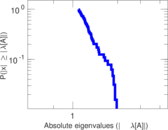
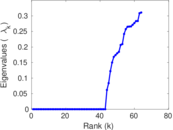
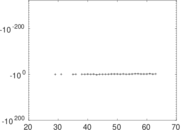
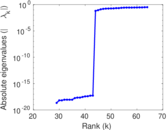
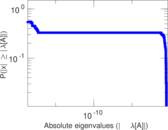
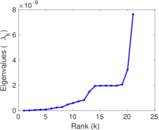
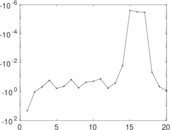
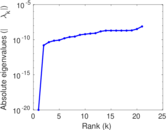
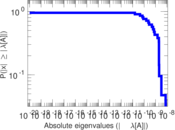
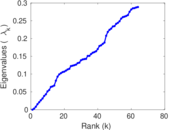
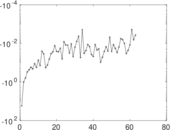
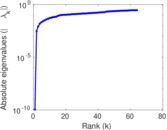
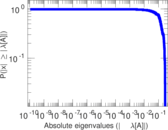
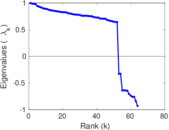
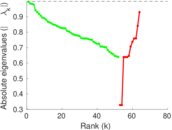
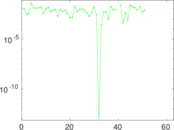
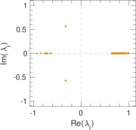
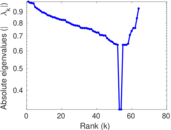
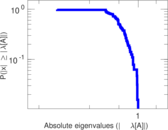
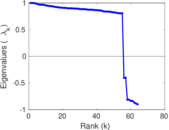
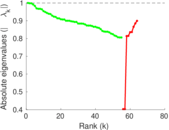
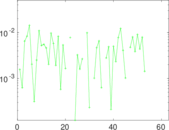
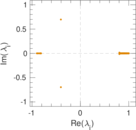
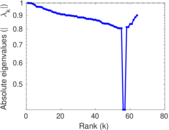
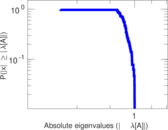
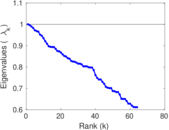
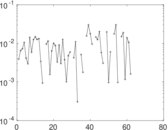
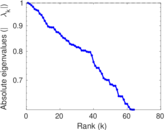
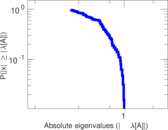
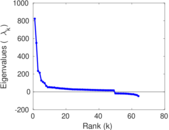
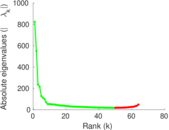
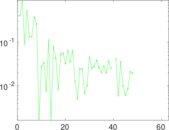
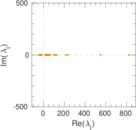
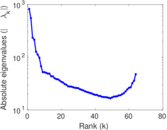
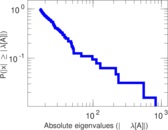
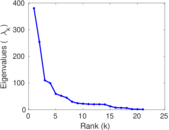
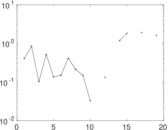
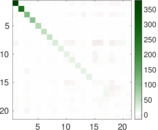
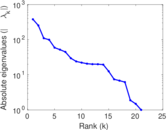
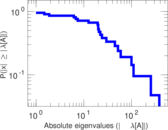
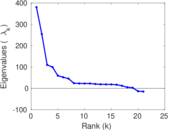
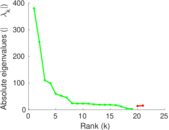
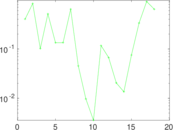
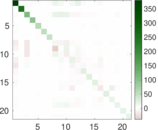
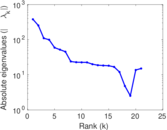
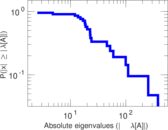
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee




















































































































































