Wikipedia links (hsb)
This network consists of the wikilinks of the Wikipedia in the Upper Sorbian
language (hsb). Nodes are Wikipedia articles, and directed edges are
wikilinks, i.e., hyperlinks within one wiki. In the wiki source, these are
indicated with [[double brackets]]. Only pages in the article namespace are
included.
Metadata
Statistics
| Size | n = | 17,665
|
| Volume | m = | 280,929
|
| Loop count | l = | 628
|
| Wedge count | s = | 119,290,498
|
| Claw count | z = | 121,106,876,651
|
| Cross count | x = | 107,761,420,894,078
|
| Triangle count | t = | 1,873,578
|
| Square count | q = | 469,149,042
|
| 4-Tour count | T4 = | 4,230,784,532
|
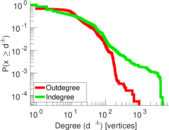
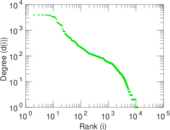
| Maximum degree | dmax = | 4,474
|
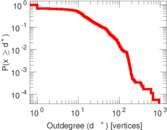
| Maximum outdegree | d+max = | 938
|
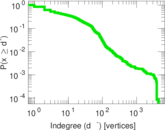
| Maximum indegree | d−max = | 4,456
|
| Average degree | d = | 31.806 3
|
| Fill | p = | 0.000 900 263
|
| Size of LCC | N = | 17,646
|
| Size of LSCC | Ns = | 9,997
|
| Relative size of LSCC | Nrs = | 0.565 921
|
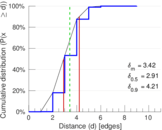
| Diameter | δ = | 11
|
| 50-Percentile effective diameter | δ0.5 = | 2.906 71
|
| 90-Percentile effective diameter | δ0.9 = | 4.212 34
|
| Median distance | δM = | 3
|
| Mean distance | δm = | 3.420 32
|
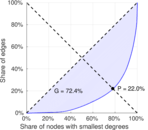
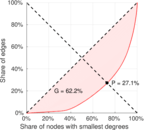
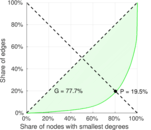
| Gini coefficient | G = | 0.723 662
|
| Balanced inequality ratio | P = | 0.219 783
|
| Outdegree balanced inequality ratio | P+ = | 0.270 791
|
| Indegree balanced inequality ratio | P− = | 0.194 779
|
| Relative edge distribution entropy | Her = | 0.872 103
|
| Power law exponent | γ = | 1.487 50
|
| Tail power law exponent | γt = | 2.651 00
|
| Tail power law exponent with p | γ3 = | 2.651 00
|
| p-value | p = | 0.001 000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 2.281 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 2.681 00
|
| Indegree p-value | pi = | 0.000 00
|
| Degree assortativity | ρ = | −0.206 720
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.777 384
|
| Clustering coefficient | c = | 0.047 118 0
|
| Directed clustering coefficient | c± = | 0.443 922
|
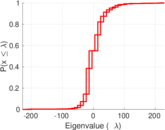
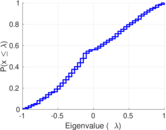
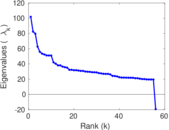
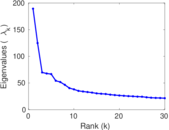
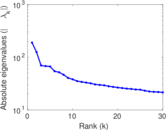
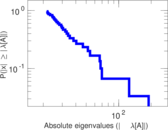
| Spectral norm | α = | 229.556
|
| Operator 2-norm | ν = | 189.558
|
| Cyclic eigenvalue | π = | 101.832
|
| Algebraic connectivity | a = | 0.076 057 7
|
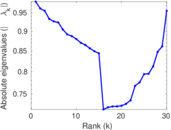
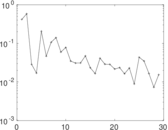
| Spectral separation | |λ1[A] / λ2[A]| = | 1.181 08
|
| Reciprocity | y = | 0.466 403
|
| Non-bipartivity | bA = | 0.189 187
|
| Normalized non-bipartivity | bN = | 0.044 765 0
|
| Algebraic non-bipartivity | χ = | 0.076 119 2
|
| Spectral bipartite frustration | bK = | 0.000 778 331
|
| Controllability | C = | 8,144
|
| Relative controllability | Cr = | 0.461 025
|
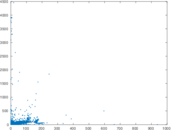
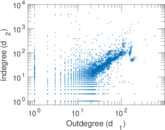
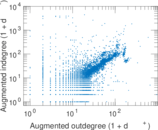
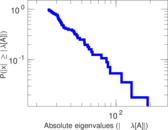
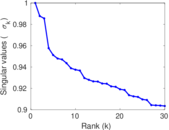
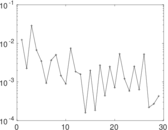
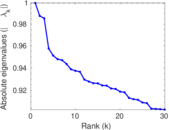
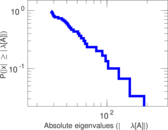
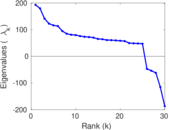
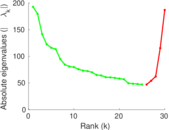
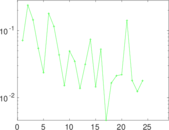
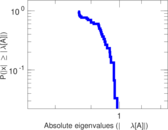
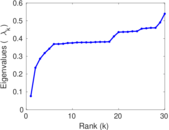
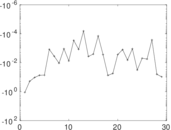
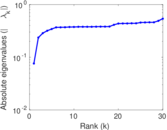
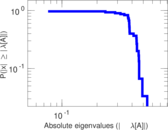
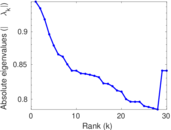
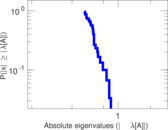
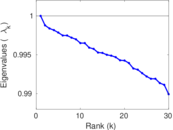
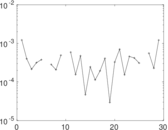
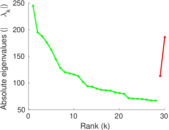
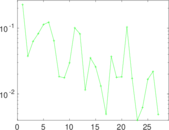
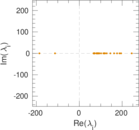
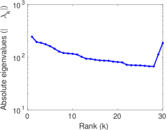
Plots

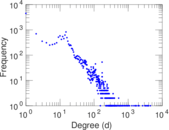
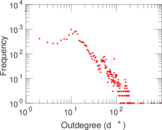
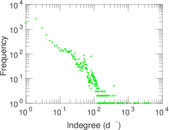
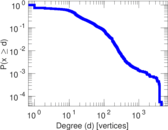
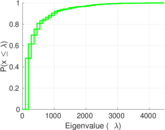

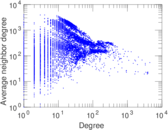
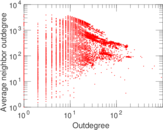
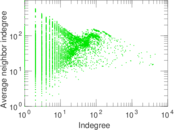
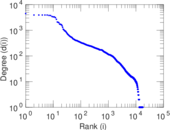
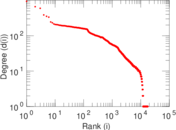

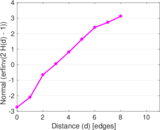
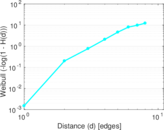
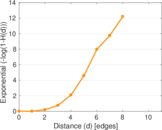



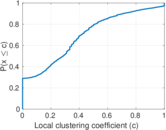
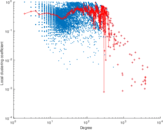

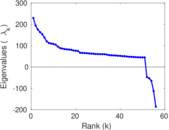
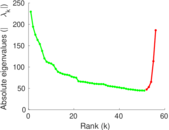
Matrix decompositions plots
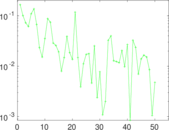
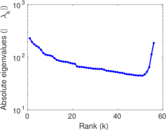
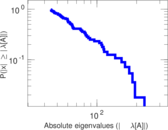
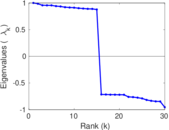
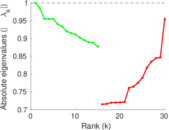
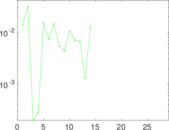
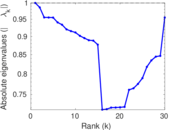
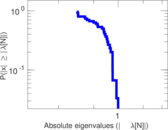
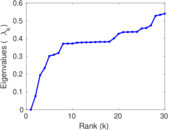
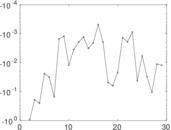
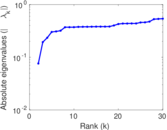
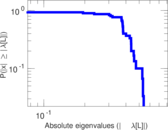
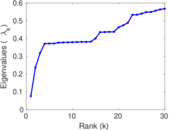
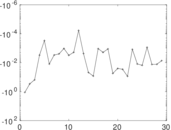
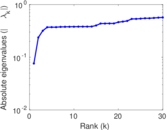
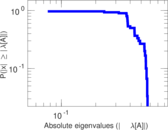
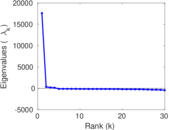
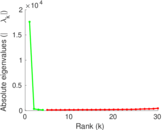
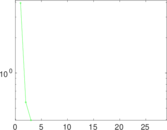
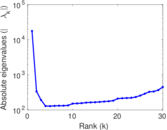
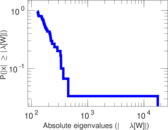
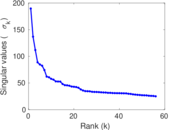
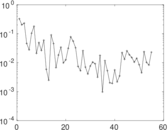
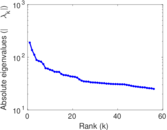
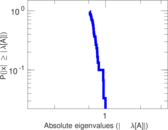
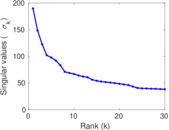
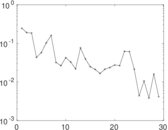
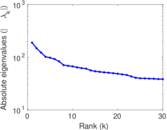
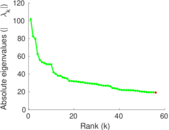
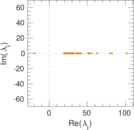
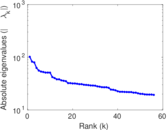
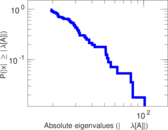
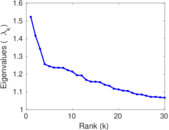
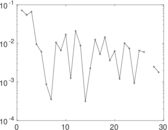
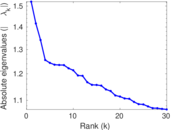
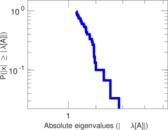
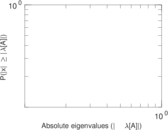
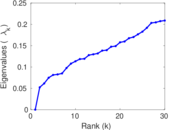
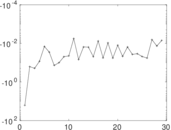

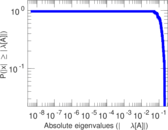
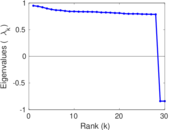
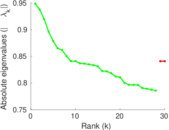
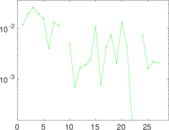
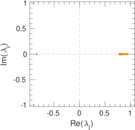
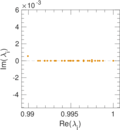
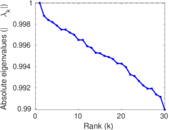
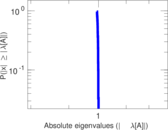
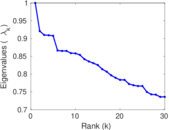
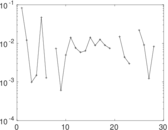
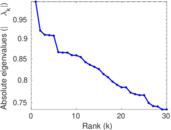
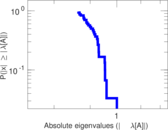
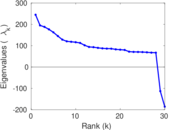
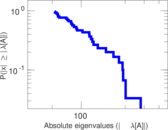
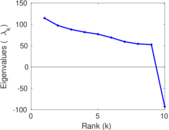
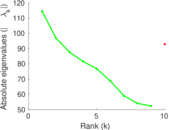
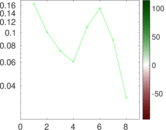
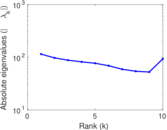
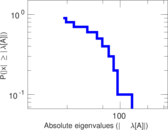
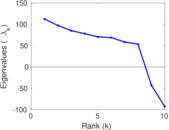
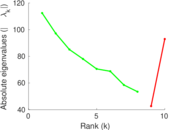
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee



















































































































































