Wikipedia links (hy)
This network consists of the wikilinks of the Wikipedia in the Armenian
language (hy). Nodes are Wikipedia articles, and directed edges are wikilinks,
i.e., hyperlinks within one wiki. In the wiki source, these are indicated with
[[double brackets]]. Only pages in the article namespace are included.
Metadata
Statistics
| Size | n = | 557,677
|
| Volume | m = | 19,197,218
|
| Loop count | l = | 241
|
| Wedge count | s = | 67,214,147,160
|
| Claw count | z = | 777,011,721,423,149
|
| Cross count | x = | 1.090 56 × 1019
|
| Triangle count | t = | 956,264,915
|
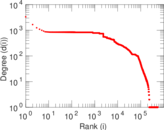
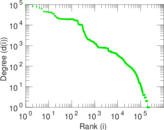
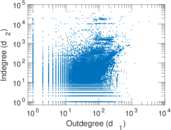
| Maximum degree | dmax = | 93,188
|
| Maximum outdegree | d+max = | 3,334
|
| Maximum indegree | d−max = | 93,182
|
| Average degree | d = | 68.847 1
|
| Fill | p = | 6.172 67 × 10−5
|
| Size of LCC | N = | 557,611
|
| Size of LSCC | Ns = | 196,074
|
| Relative size of LSCC | Nrs = | 0.351 591
|
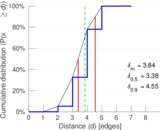
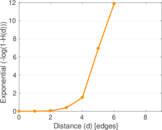
| Diameter | δ = | 9
|
| 50-Percentile effective diameter | δ0.5 = | 3.381 86
|
| 90-Percentile effective diameter | δ0.9 = | 4.547 38
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 3.841 10
|
| Gini coefficient | G = | 0.868 276
|
| Balanced inequality ratio | P = | 0.139 796
|
| Outdegree balanced inequality ratio | P+ = | 0.157 712
|
| Indegree balanced inequality ratio | P− = | 0.153 099
|
| Relative edge distribution entropy | Her = | 0.840 904
|
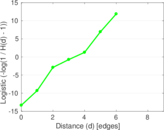
| Power law exponent | γ = | 1.596 24
|
| Degree assortativity | ρ = | −0.144 636
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.794 643
|
| Clustering coefficient | c = | 0.042 681 4
|
| Directed clustering coefficient | c± = | 0.846 532
|
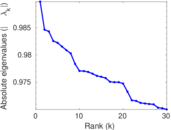
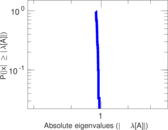
| Spectral norm | α = | 1,632.43
|
| Operator 2-norm | ν = | 1,462.95
|
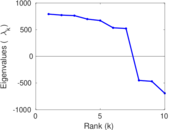
| Cyclic eigenvalue | π = | 807.017
|
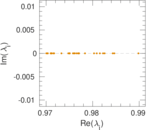
| Spectral separation | |λ1[A] / λ2[A]| = | 1.044 83
|
| Reciprocity | y = | 0.500 510
|
| Non-bipartivity | bA = | 0.150 866
|
| Normalized non-bipartivity | bN = | 0.045 708 8
|
| Algebraic non-bipartivity | χ = | 0.125 399
|
| Spectral bipartite frustration | bK = | 0.000 607 271
|
| Controllability | C = | 338,499
|
| Relative controllability | Cr = | 0.606 980
|
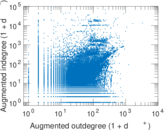
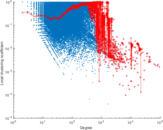
Plots
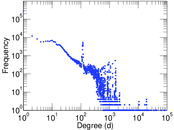
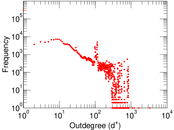
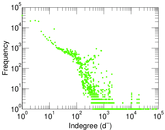
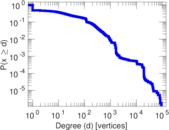
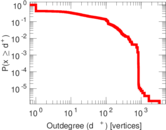
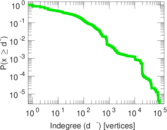
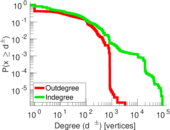

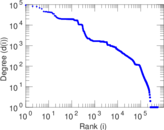
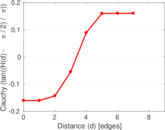
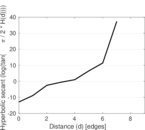
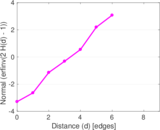
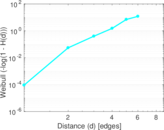
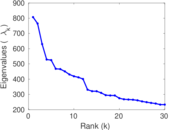
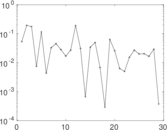
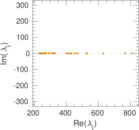
Matrix decompositions plots
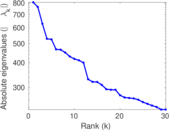
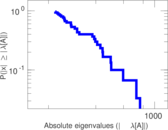
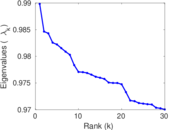
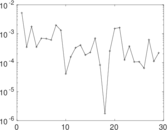
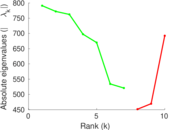
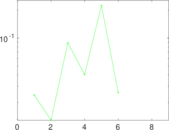
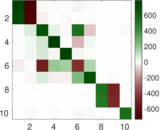
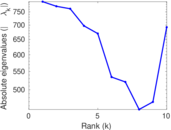
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee





































