Wikipedia links (mhr)
This network consists of the wikilinks of the Wikipedia in the Eastern Mari
language (mhr). Nodes are Wikipedia articles, and directed edges are
wikilinks, i.e., hyperlinks within one wiki. In the wiki source, these are
indicated with [[double brackets]]. Only pages in the article namespace are
included.
Metadata
Statistics
| Size | n = | 14,569
|
| Volume | m = | 226,643
|
| Loop count | l = | 4
|
| Wedge count | s = | 88,003,229
|
| Claw count | z = | 88,057,115,160
|
| Cross count | x = | 79,020,397,787,306
|
| Triangle count | t = | 1,285,364
|
| Square count | q = | 362,046,172
|
| 4-Tour count | T4 = | 3,248,747,202
|
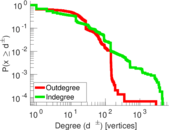
| Maximum degree | dmax = | 4,635
|
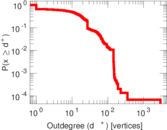
| Maximum outdegree | d+max = | 2,936
|
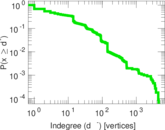
| Maximum indegree | d−max = | 4,534
|
| Average degree | d = | 31.113 0
|
| Fill | p = | 0.001 067 78
|
| Size of LCC | N = | 14,549
|
| Size of LSCC | Ns = | 7,486
|
| Relative size of LSCC | Nrs = | 0.513 831
|
| Diameter | δ = | 10
|
| 50-Percentile effective diameter | δ0.5 = | 2.726 91
|
| 90-Percentile effective diameter | δ0.9 = | 3.937 43
|
| Median distance | δM = | 3
|
| Mean distance | δm = | 3.286 36
|
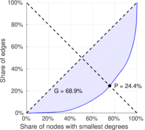
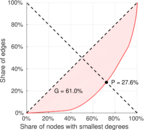
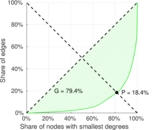
| Gini coefficient | G = | 0.689 080
|
| Balanced inequality ratio | P = | 0.244 439
|
| Outdegree balanced inequality ratio | P+ = | 0.276 064
|
| Indegree balanced inequality ratio | P− = | 0.184 056
|
| Relative edge distribution entropy | Her = | 0.880 059
|
| Power law exponent | γ = | 1.461 22
|
| Tail power law exponent | γt = | 2.731 00
|
| Tail power law exponent with p | γ3 = | 2.731 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 3.261 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 2.221 00
|
| Indegree p-value | pi = | 0.000 00
|
| Degree assortativity | ρ = | −0.180 448
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.580 294
|
| Clustering coefficient | c = | 0.043 817 6
|
| Directed clustering coefficient | c± = | 0.523 602
|
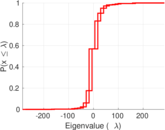
| Spectral norm | α = | 285.076
|
| Operator 2-norm | ν = | 177.983
|
| Cyclic eigenvalue | π = | 142.022
|
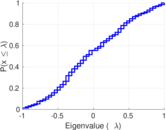
| Algebraic connectivity | a = | 0.120 443
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.460 55
|
| Reciprocity | y = | 0.389 917
|
| Non-bipartivity | bA = | 0.365 320
|
| Normalized non-bipartivity | bN = | 0.075 984 9
|
| Algebraic non-bipartivity | χ = | 0.120 441
|
| Spectral bipartite frustration | bK = | 0.001 200 54
|
| Controllability | C = | 6,511
|
| Relative controllability | Cr = | 0.446 908
|
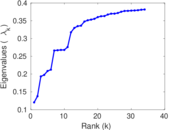
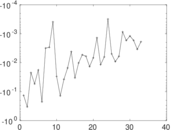
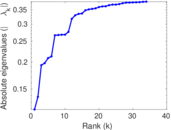
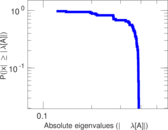
Plots

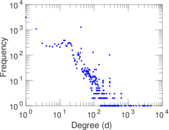
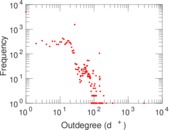
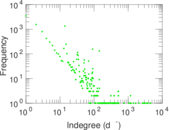
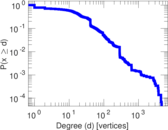
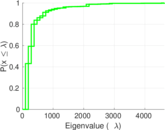



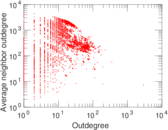
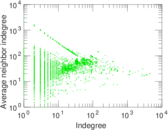
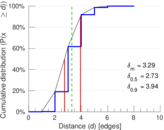
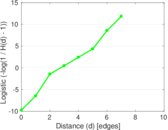
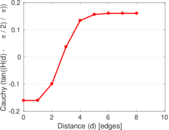
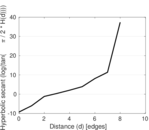
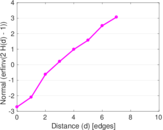
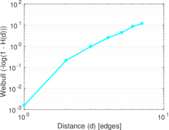



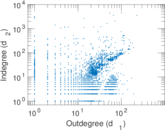
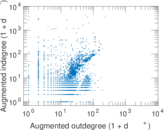
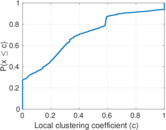
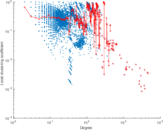

Matrix decompositions plots
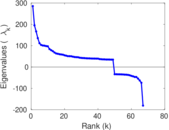
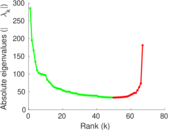
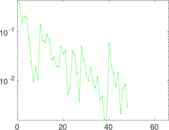
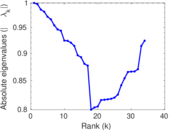
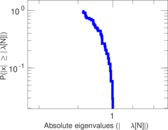
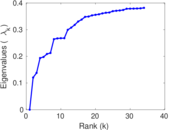
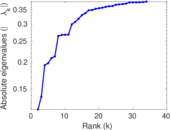
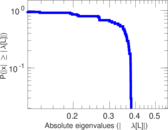
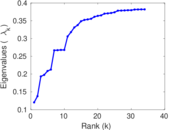
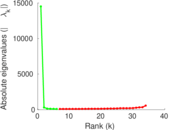
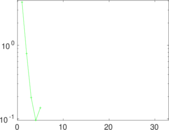
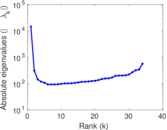
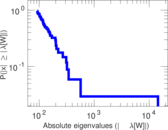
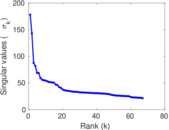
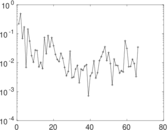
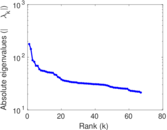
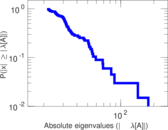
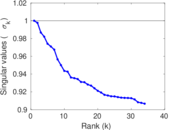
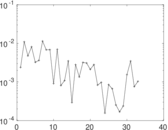
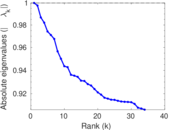
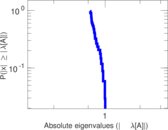
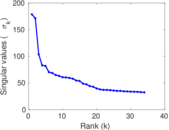
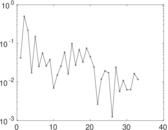
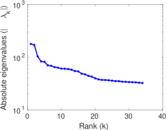
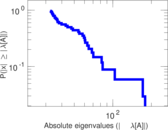
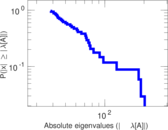
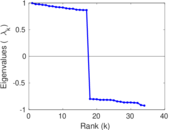
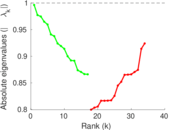
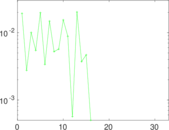
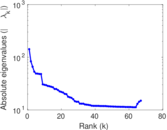
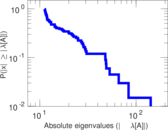
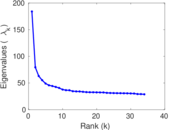
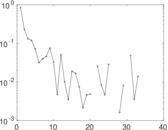
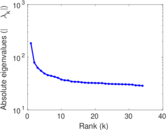
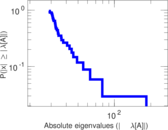
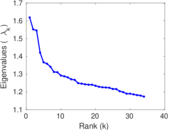
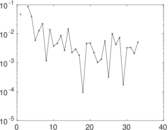
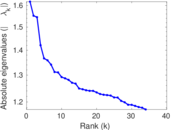
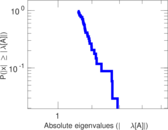
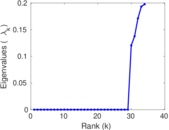
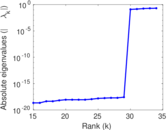
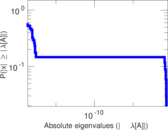
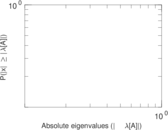
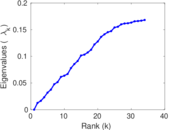
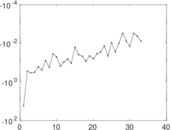
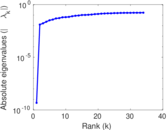
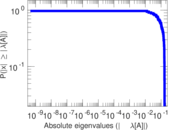
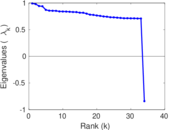
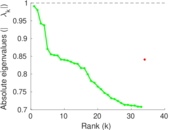
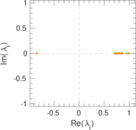
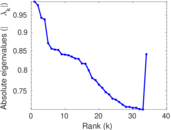
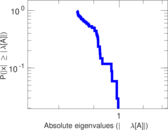
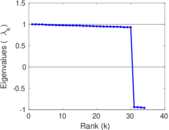
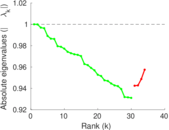
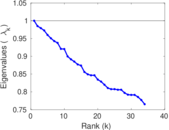
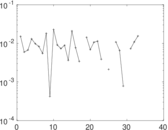
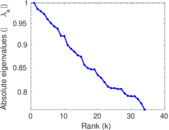
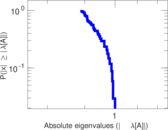
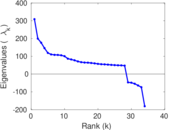
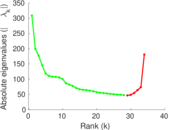
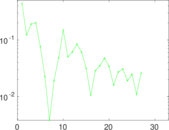
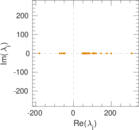
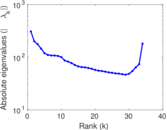
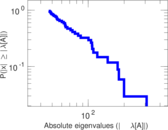
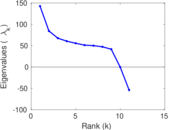
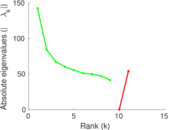
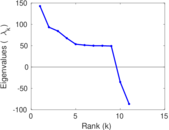
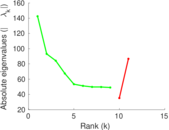
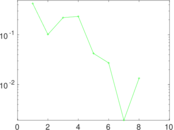
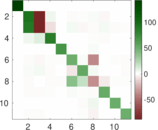
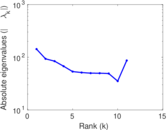
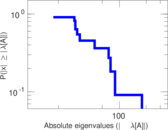
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee





















































































































































