Wikipedia links (pnb)
This network consists of the wikilinks of the Wikipedia in the Western Punjabi
language (pnb). Nodes are Wikipedia articles, and directed edges are
wikilinks, i.e., hyperlinks within one wiki. In the wiki source, these are
indicated with [[double brackets]]. Only pages in the article namespace are
included.
Metadata
Statistics
| Size | n = | 51,933
|
| Volume | m = | 1,436,320
|
| Loop count | l = | 14
|
| Wedge count | s = | 755,607,228
|
| Claw count | z = | 2,184,922,413,634
|
| Cross count | x = | 6,947,913,867,227,964
|
| Triangle count | t = | 34,753,879
|
| Square count | q = | 8,317,395,621
|
| 4-Tour count | T4 = | 69,423,952,216
|
| Maximum degree | dmax = | 16,696
|
| Maximum outdegree | d+max = | 1,338
|
| Maximum indegree | d−max = | 16,688
|
| Average degree | d = | 55.314 3
|
| Fill | p = | 0.000 532 555
|
| Size of LCC | N = | 51,897
|
| Size of LSCC | Ns = | 31,908
|
| Relative size of LSCC | Nrs = | 0.614 407
|
| Diameter | δ = | 9
|
| 50-Percentile effective diameter | δ0.5 = | 2.910 35
|
| 90-Percentile effective diameter | δ0.9 = | 3.909 59
|
| Median distance | δM = | 3
|
| Mean distance | δm = | 3.376 74
|
| Gini coefficient | G = | 0.746 451
|
| Balanced inequality ratio | P = | 0.194 055
|
| Outdegree balanced inequality ratio | P+ = | 0.219 541
|
| Indegree balanced inequality ratio | P− = | 0.178 613
|
| Relative edge distribution entropy | Her = | 0.885 332
|
| Power law exponent | γ = | 1.386 75
|
| Tail power law exponent | γt = | 1.711 00
|
| Degree assortativity | ρ = | −0.081 327 9
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| Clustering coefficient | c = | 0.137 984
|
| Directed clustering coefficient | c± = | 0.832 105
|
| Algebraic connectivity | a = | 0.038 090 2
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.158 24
|
| Reciprocity | y = | 0.580 577
|
| Non-bipartivity | bA = | 0.688 527
|
| Normalized non-bipartivity | bN = | 0.057 390 7
|
| Spectral bipartite frustration | bK = | 0.000 694 119
|
| Controllability | C = | 28,115
|
| Relative controllability | Cr = | 0.541 371
|
Plots

















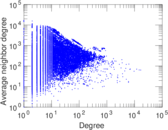
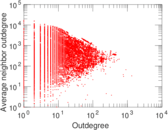
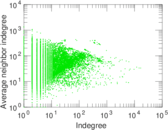





















Matrix decompositions plots

































































































Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee









































































































































