Wikipedia links (roa-tara)
This network consists of the wikilinks of the Wikipedia in the Tarantino
language (roa-tara). Nodes are Wikipedia articles, and directed edges are
wikilinks, i.e., hyperlinks within one wiki. In the wiki source, these are
indicated with [[double brackets]]. Only pages in the article namespace are
included.
Metadata
Statistics
| Size | n = | 10,423
|
| Volume | m = | 1,089,948
|
| Loop count | l = | 37
|
| Wedge count | s = | 309,344,121
|
| Claw count | z = | 598,397,119,902
|
| Cross count | x = | 1,125,458,167,871,816
|
| Triangle count | t = | 32,943,400
|
| Square count | q = | 5,588,314,508
|
| 4-Tour count | T4 = | 45,945,120,166
|
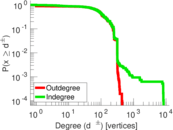
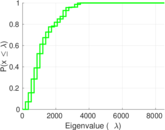
| Maximum degree | dmax = | 8,528
|
| Maximum outdegree | d+max = | 449
|
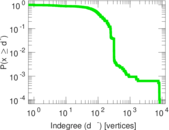
| Maximum indegree | d−max = | 8,443
|
| Average degree | d = | 209.143
|
| Fill | p = | 0.010 032 8
|
| Size of LCC | N = | 10,412
|
| Size of LSCC | Ns = | 9,265
|
| Relative size of LSCC | Nrs = | 0.888 900
|
| Diameter | δ = | 10
|
| 50-Percentile effective diameter | δ0.5 = | 1.710 51
|
| 90-Percentile effective diameter | δ0.9 = | 2.766 93
|
| Median distance | δM = | 2
|
| Mean distance | δm = | 2.336 82
|
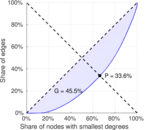
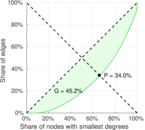
| Gini coefficient | G = | 0.455 401
|
| Balanced inequality ratio | P = | 0.336 066
|
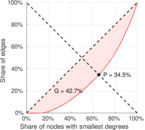
| Outdegree balanced inequality ratio | P+ = | 0.345 103
|
| Indegree balanced inequality ratio | P− = | 0.339 865
|
| Relative edge distribution entropy | Her = | 0.957 496
|
| Power law exponent | γ = | 1.238 24
|
| Tail power law exponent | γt = | 2.211 00
|
| Tail power law exponent with p | γ3 = | 2.211 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 2.271 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 2.251 00
|
| Indegree p-value | pi = | 0.000 00
|
| Degree assortativity | ρ = | −0.053 811 8
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.735 338
|
| Clustering coefficient | c = | 0.319 483
|
| Directed clustering coefficient | c± = | 0.945 002
|
| Spectral norm | α = | 625.465
|
| Operator 2-norm | ν = | 319.967
|
| Cyclic eigenvalue | π = | 309.020
|
| Algebraic connectivity | a = | 0.158 820
|
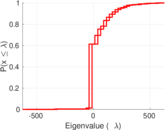
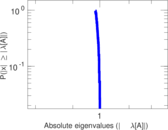
| Spectral separation | |λ1[A] / λ2[A]| = | 1.260 55
|
| Reciprocity | y = | 0.873 657
|
| Non-bipartivity | bA = | 0.761 273
|
| Normalized non-bipartivity | bN = | 0.116 968
|
| Algebraic non-bipartivity | χ = | 0.191 104
|
| Spectral bipartite frustration | bK = | 0.000 405 190
|
| Controllability | C = | 955
|
| Relative controllability | Cr = | 0.091 624 3
|
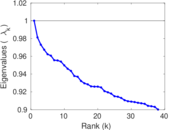
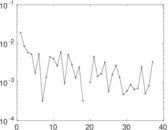
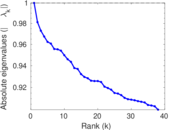
Plots

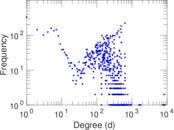

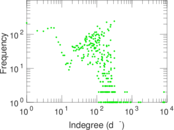
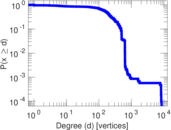
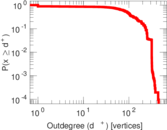


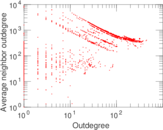

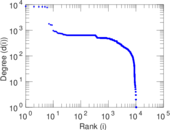
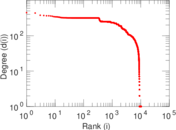
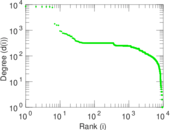


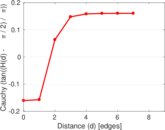



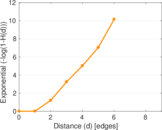





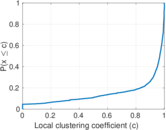
Matrix decompositions plots
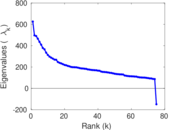
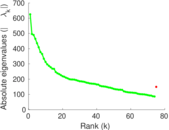
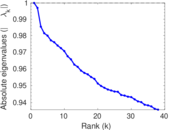
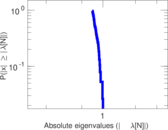
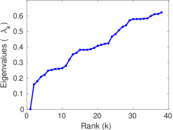

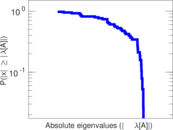
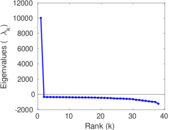
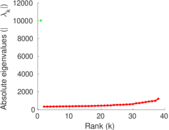
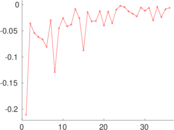
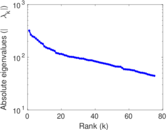
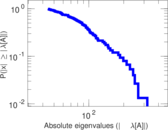
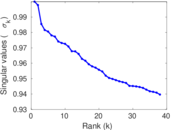
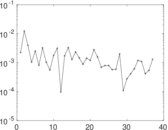
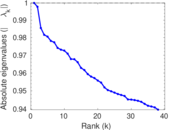
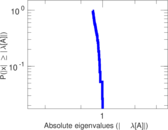
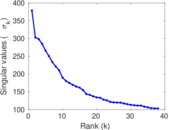
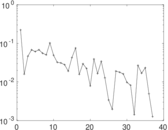
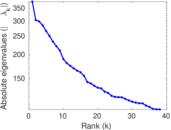
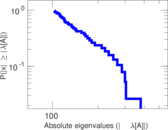
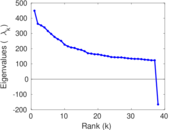
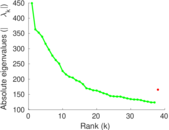
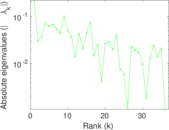
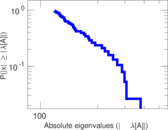
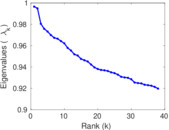
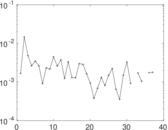
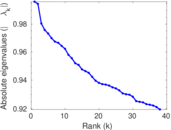
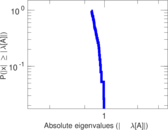
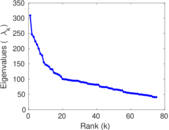
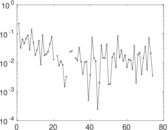
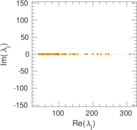
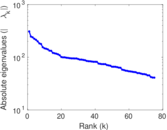

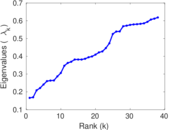
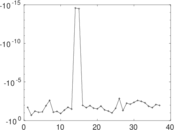


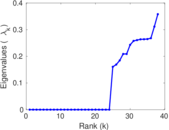
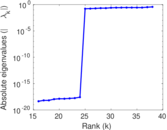

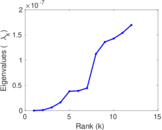
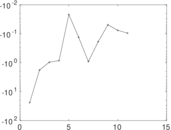
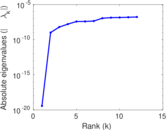
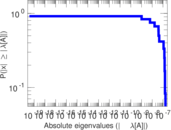
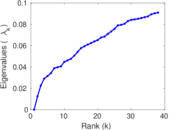
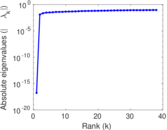
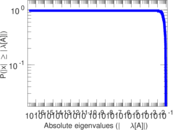
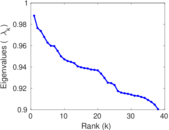
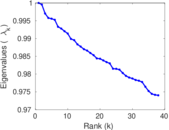
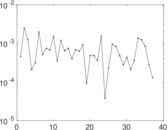
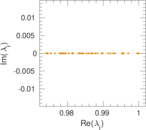
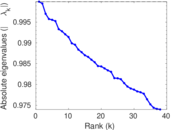

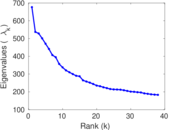
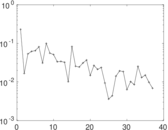
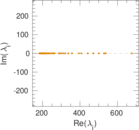
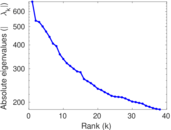
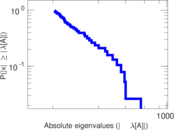
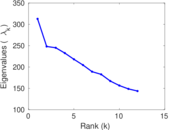
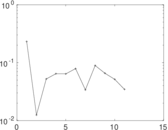
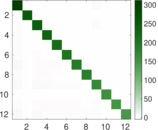
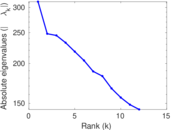
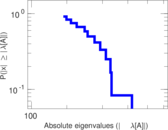
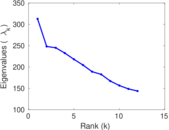
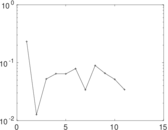
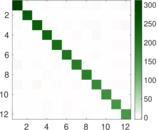
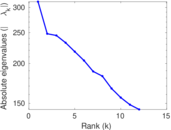

Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee











































































































































