Wikipedia links (sco)

This network consists of the wikilinks of the Wikipedia in the Scots language (sco). Nodes are Wikipedia articles, and directed edges are wikilinks, i.e., hyperlinks within one wiki. In the wiki source, these are indicated with [[double brackets]]. Only pages in the article namespace are included.

Metadata

CodeWsco
Internal namewikipedia_link_sco
NameWikipedia links (sco)
Data sourcehttp://dumps.wikimedia.org/
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Hyperlink network
Node meaningArticle
Edge meaningWikilink
Network formatUnipartite, directed
Edge typeUnweighted, no multiple edges
ReciprocalContains reciprocal edges
Directed cyclesContains directed cycles
LoopsContains loops

Statistics

Size n =64,347
Volume m =1,397,072
Wedge count s =412,953,327
Claw count z =633,118,413,573
Triangle count t =16,471,247
Square count q =2,157,090,491
4-Tour count T4 =15,974,561,712
Maximum degree dmax =10,803
Maximum outdegree d+max =644
Maximum indegree d−max =10,802
Average degree d =43.423 1
Size of LCC N =64,278
Size of LSCC Ns =46,609
Relative size of LSCC Nrs =0.724 338
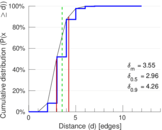
Diameter δ =13
50-Percentile effective diameter δ0.5 =2.955 86
90-Percentile effective diameter δ0.9 =4.256 89
Median distance δM =3
Mean distance δm =3.551 26
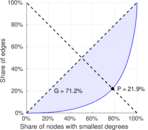
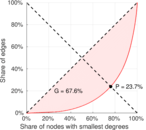
Gini coefficient G =0.711 634
Balanced inequality ratio P =0.218 703
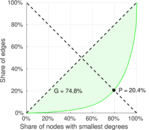
Outdegree balanced inequality ratio P+ =0.237 437
Indegree balanced inequality ratio P− =0.204 168
Relative edge distribution entropy Her =0.903 987
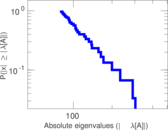
Power law exponent γ =1.409 50
Tail power law exponent γt =2.061 00
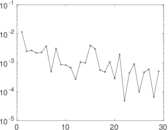
Degree assortativity ρ =−0.065 841 0
Degree assortativity p-value pρ =0.000 00
In/outdegree correlation ρ± =+0.681 845
Clustering coefficient c =0.119 659
Directed clustering coefficient c± =0.708 254
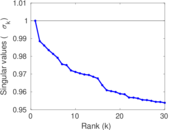
Operator 2-norm ν =219.582
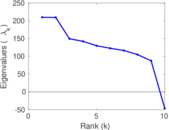
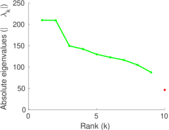
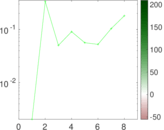
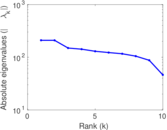
Cyclic eigenvalue π =208.042
Algebraic connectivity a =0.090 046 5
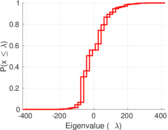
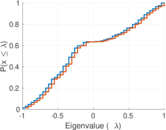
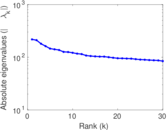
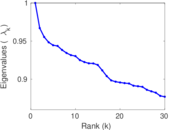
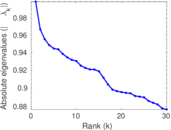
Spectral separation |λ1[A] / λ2[A]| =1.004 68
Reciprocity y =0.507 068
Non-bipartivity bA =0.607 506
Normalized non-bipartivity bN =0.050 117 1
Spectral bipartite frustration bK =0.000 693 951

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Delaunay graph drawing

In/outdegree scatter plot

Clustering coefficient distribution

Average neighbor degree distribution

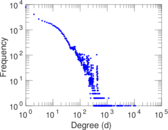
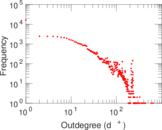
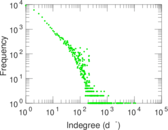
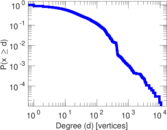
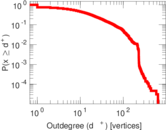
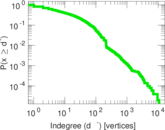
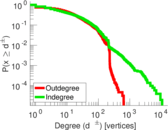
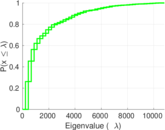
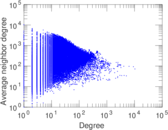
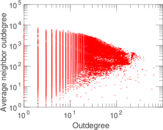
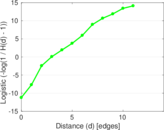
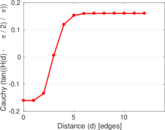
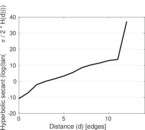
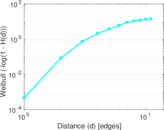
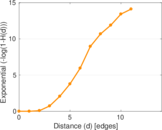
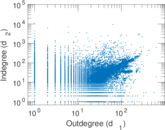
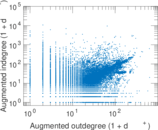
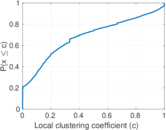
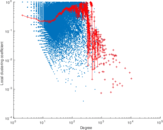
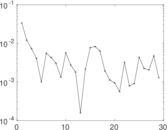
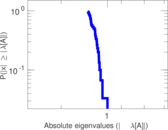
Matrix decompositions plots

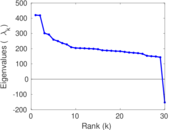
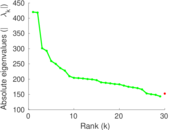
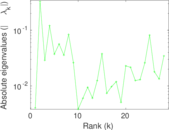
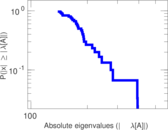
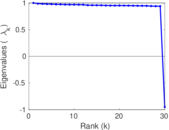
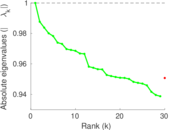
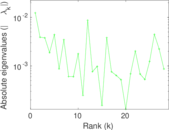
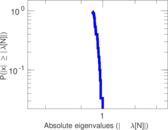
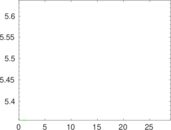
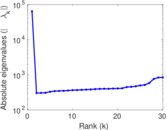
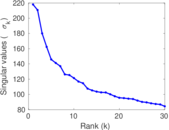
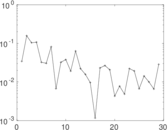
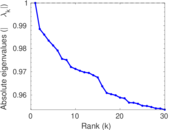
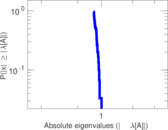
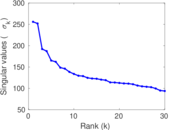
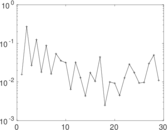
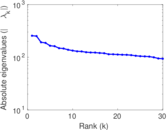
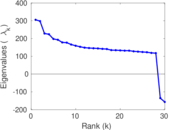
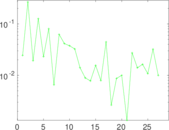
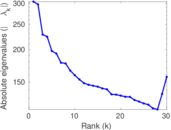
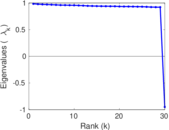
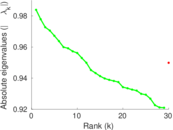
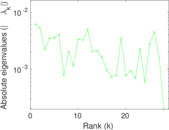
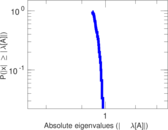
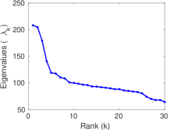
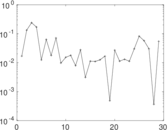
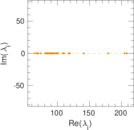
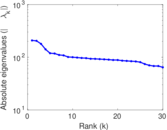
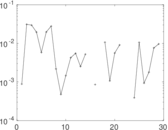
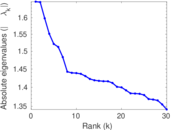
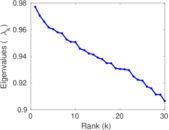
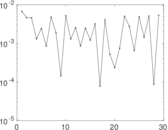
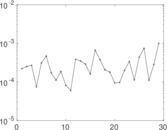
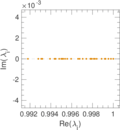
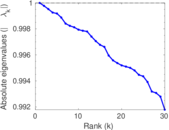
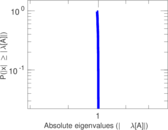
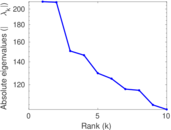
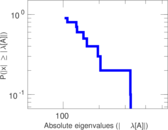
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]