Wikipedia links (vec)
This network consists of the wikilinks of the Wikipedia in the Venetian
language (vec). Nodes are Wikipedia articles, and directed edges are
wikilinks, i.e., hyperlinks within one wiki. In the wiki source, these are
indicated with [[double brackets]]. Only pages in the article namespace are
included.
Metadata
Statistics
| Size | n = | 17,524
|
| Volume | m = | 293,008
|
| Loop count | l = | 136
|
| Wedge count | s = | 65,643,738
|
| Claw count | z = | 42,682,121,641
|
| Cross count | x = | 26,682,295,604,888
|
| Triangle count | t = | 2,656,022
|
| Square count | q = | 415,788,871
|
| 4-Tour count | T4 = | 3,589,321,046
|
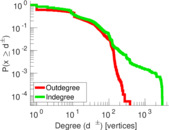
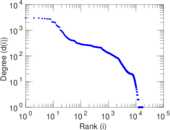
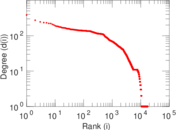
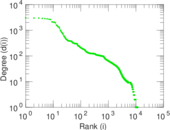
| Maximum degree | dmax = | 3,011
|
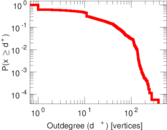
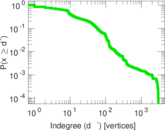
| Maximum outdegree | d+max = | 384
|
| Maximum indegree | d−max = | 3,011
|
| Average degree | d = | 33.440 8
|
| Fill | p = | 0.000 954 142
|
| Size of LCC | N = | 17,493
|
| Size of LSCC | Ns = | 10,849
|
| Relative size of LSCC | Nrs = | 0.619 094
|
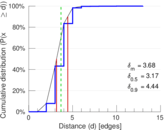
| Diameter | δ = | 15
|
| 50-Percentile effective diameter | δ0.5 = | 3.167 86
|
| 90-Percentile effective diameter | δ0.9 = | 4.440 03
|
| Median distance | δM = | 4
|
| Mean distance | δm = | 3.677 24
|
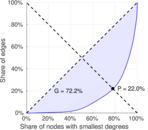
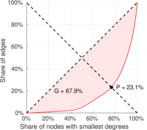
| Gini coefficient | G = | 0.721 509
|
| Balanced inequality ratio | P = | 0.219 651
|
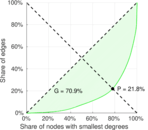
| Outdegree balanced inequality ratio | P+ = | 0.230 697
|
| Indegree balanced inequality ratio | P− = | 0.218 001
|
| Relative edge distribution entropy | Her = | 0.886 480
|
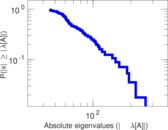
| Power law exponent | γ = | 1.505 78
|
| Tail power law exponent | γt = | 2.671 00
|
| Tail power law exponent with p | γ3 = | 2.671 00
|
| p-value | p = | 0.000 00
|
| Outdegree tail power law exponent with p | γ3,o = | 2.961 00
|
| Outdegree p-value | po = | 0.000 00
|
| Indegree tail power law exponent with p | γ3,i = | 2.451 00
|
| Indegree p-value | pi = | 0.000 00
|
| Degree assortativity | ρ = | −0.117 668
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| In/outdegree correlation | ρ± = | +0.777 922
|
| Clustering coefficient | c = | 0.121 383
|
| Directed clustering coefficient | c± = | 0.645 892
|
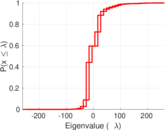
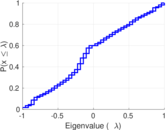
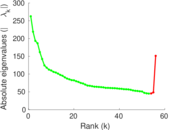
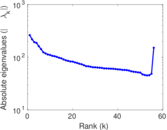
| Spectral norm | α = | 262.461
|
| Operator 2-norm | ν = | 189.343
|
| Cyclic eigenvalue | π = | 114.346
|
| Algebraic connectivity | a = | 0.025 646 5
|
| Spectral separation | |λ1[A] / λ2[A]| = | 1.197 77
|
| Reciprocity | y = | 0.514 505
|
| Non-bipartivity | bA = | 0.423 768
|
| Normalized non-bipartivity | bN = | 0.070 440 6
|
| Algebraic non-bipartivity | χ = | 0.121 559
|
| Spectral bipartite frustration | bK = | 0.001 221 07
|
| Controllability | C = | 6,724
|
| Relative controllability | Cr = | 0.383 702
|
Plots

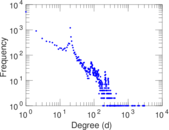
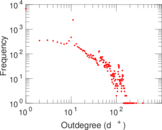
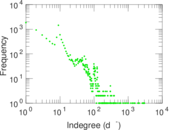
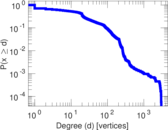
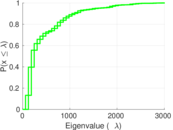


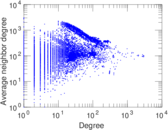

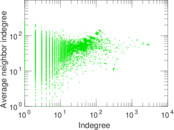
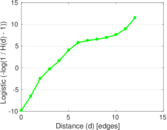
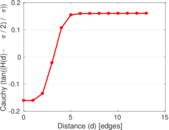
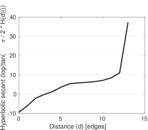
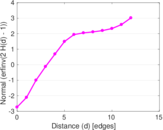
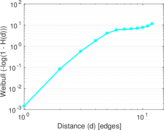
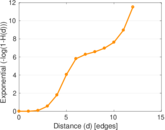




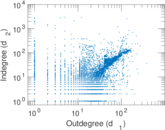
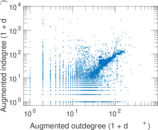
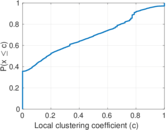
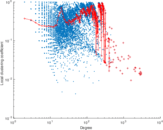

Matrix decompositions plots

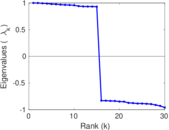
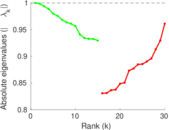
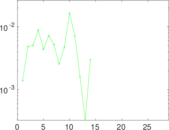
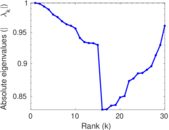
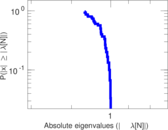
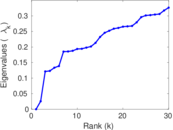
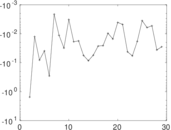
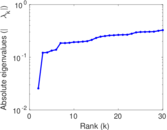
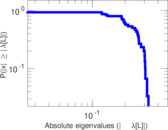
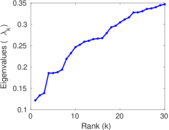
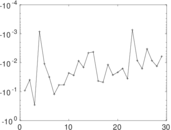
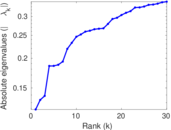
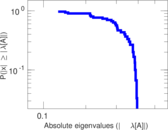
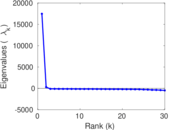
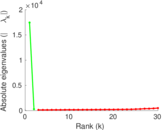
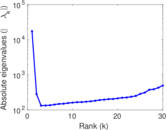
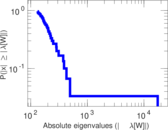
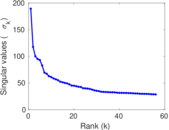

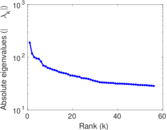
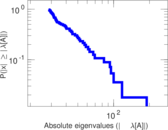

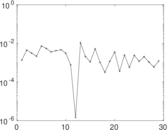
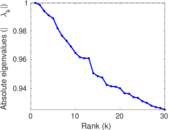
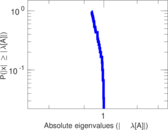
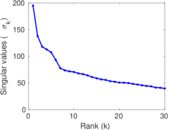
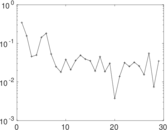
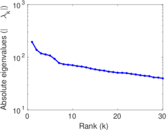
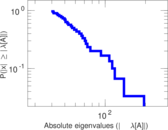
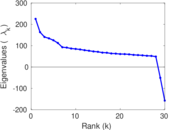
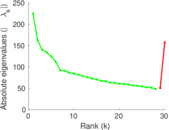
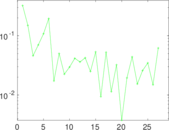
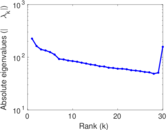
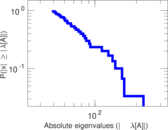
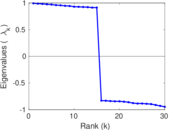
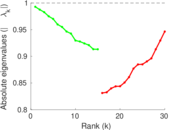
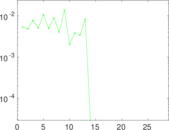

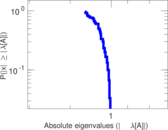
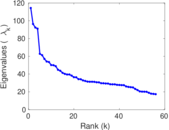
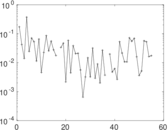
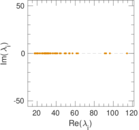
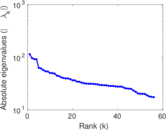
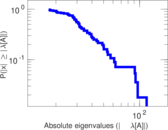
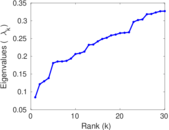
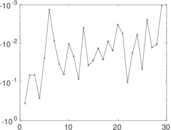
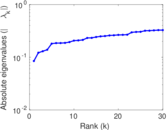
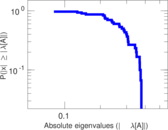
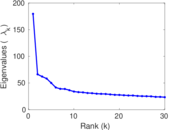
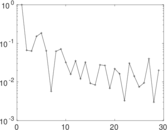
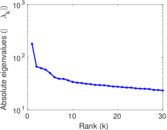
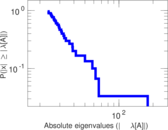
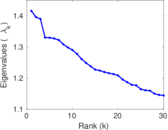
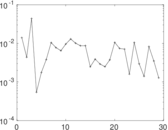
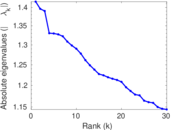
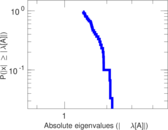


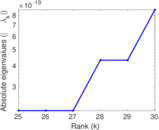
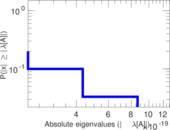

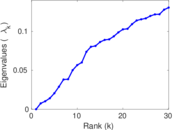
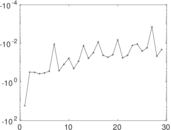

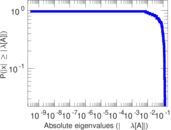
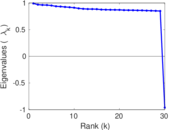

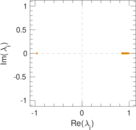
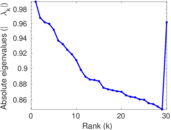

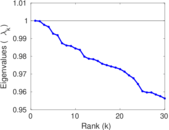
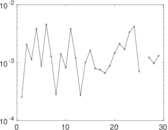
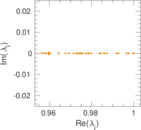
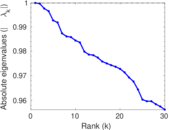


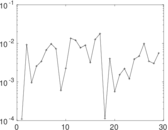
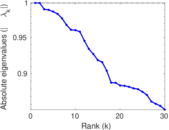
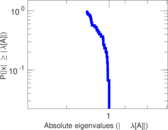
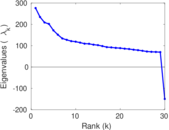
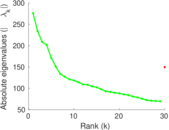
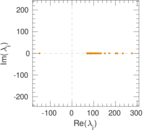
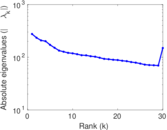
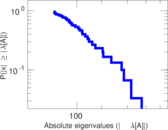
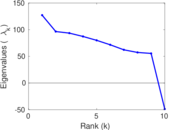
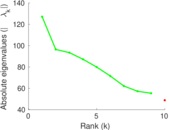
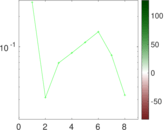
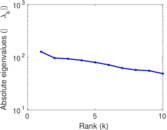
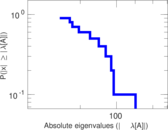
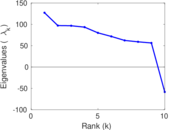


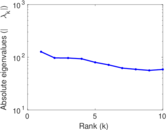

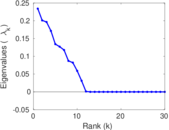
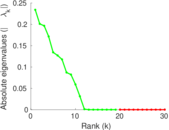
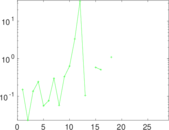
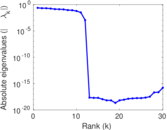
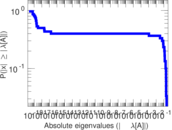
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee





















































































































































