Wikispeedia
These are paths from the Wikispeedia game, in which users are tasked to find a
article of the English Wikipedia, starting from a given article of the English
Wikipedia, being allowed to only click links. Nodes are articles of the
English Wikipedia, and edges represent clicks.
Metadata
Statistics
| Size | n = | 4,179
|
| Volume | m = | 343,950
|
| Unique edge count | m̿ = | 57,572
|
| Loop count | l = | 0
|
| Wedge count | s = | 5,350,052
|
| Claw count | z = | 1,231,596,321
|
| Cross count | x = | 314,843,715,024
|
| Triangle count | t = | 119,886
|
| Square count | q = | 4,843,415
|
| 4-Tour count | T4 = | 60,248,528
|
| Maximum degree | dmax = | 23,348
|
| Maximum outdegree | d+max = | 11,557
|
| Maximum indegree | d−max = | 11,791
|
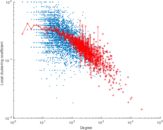
| Average degree | d = | 164.609
|
| Fill | p = | 0.003 297 39
|
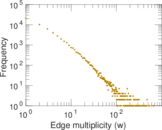
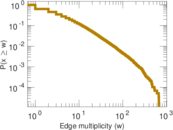
| Average edge multiplicity | m̃ = | 5.974 26
|
| Size of LCC | N = | 4,179
|
| Size of LSCC | Ns = | 3,766
|
| Relative size of LSCC | Nrs = | 0.901 173
|
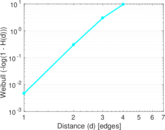
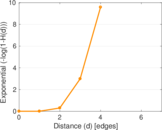
| Diameter | δ = | 5
|
| 50-Percentile effective diameter | δ0.5 = | 2.346 75
|
| 90-Percentile effective diameter | δ0.9 = | 2.927 82
|
| Median distance | δM = | 3
|
| Mean distance | δm = | 2.784 22
|
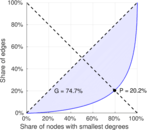
| Gini coefficient | G = | 0.747 283
|
| Balanced inequality ratio | P = | 0.202 138
|
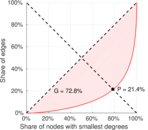
| Outdegree balanced inequality ratio | P+ = | 0.214 360
|
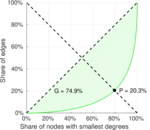
| Indegree balanced inequality ratio | P− = | 0.203 096
|
| Relative edge distribution entropy | Her = | 0.919 506
|
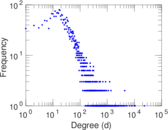
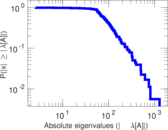
| Power law exponent | γ = | 1.382 01
|
| Tail power law exponent | γt = | 2.571 00
|
| Tail power law exponent with p | γ3 = | 2.571 00
|
| p-value | p = | 0.017 000 0
|
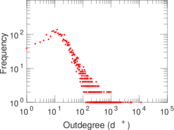
| Outdegree tail power law exponent with p | γ3,o = | 3.491 00
|
| Outdegree p-value | po = | 0.055 000 0
|
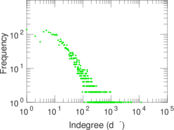
| Indegree tail power law exponent with p | γ3,i = | 2.641 00
|
| Indegree p-value | pi = | 0.765 000
|
| Degree assortativity | ρ = | −0.115 584
|
| Degree assortativity p-value | pρ = | 2.328 89 × 10−297
|
| In/outdegree correlation | ρ± = | +0.899 184
|
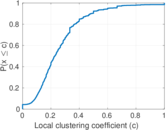
| Clustering coefficient | c = | 0.067 225 1
|
| Directed clustering coefficient | c± = | 0.075 007 8
|
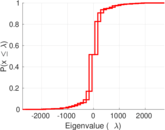
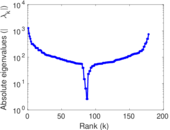
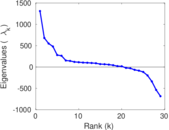
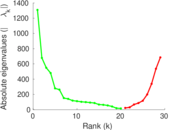
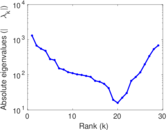
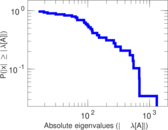
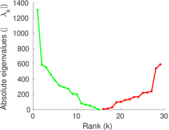
| Spectral norm | α = | 2,742.02
|
| Operator 2-norm | ν = | 1,474.05
|
| Cyclic eigenvalue | π = | 1,275.36
|
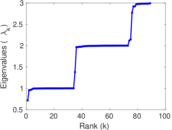
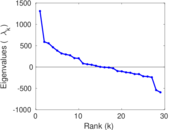
| Algebraic connectivity | a = | 0.716 505
|
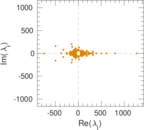
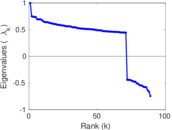
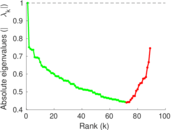
| Spectral separation | |λ1[A] / λ2[A]| = | 1.392 30
|
| Reciprocity | y = | 0.245 675
|
| Non-bipartivity | bA = | 0.281 762
|
| Normalized non-bipartivity | bN = | 0.382 642
|
| Algebraic non-bipartivity | χ = | 0.620 422
|
| Spectral bipartite frustration | bK = | 0.006 417 68
|
| Controllability | C = | 644
|
| Relative controllability | Cr = | 0.154 104
|
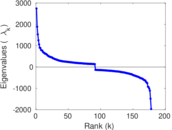
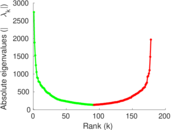
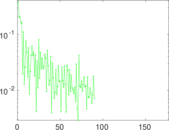
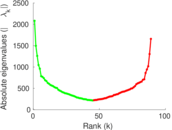
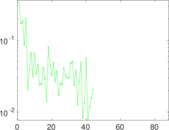
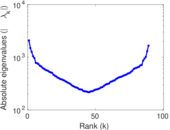
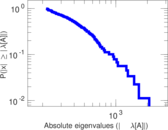
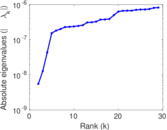
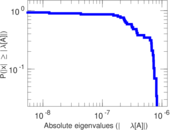
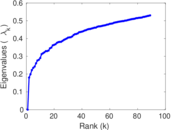
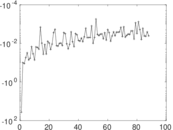
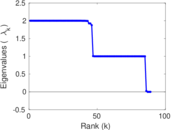
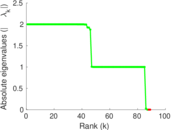
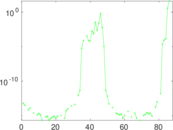
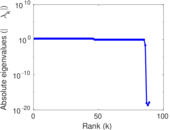
Plots

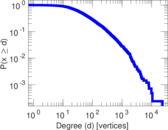
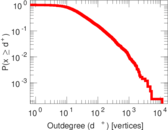
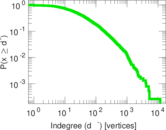
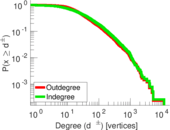
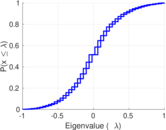
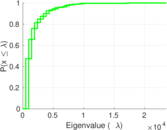
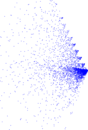
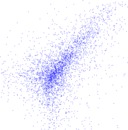
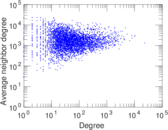
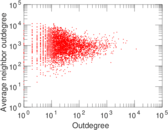
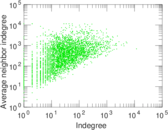
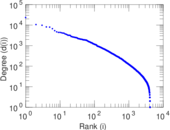
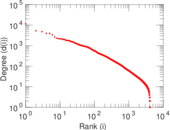
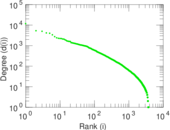
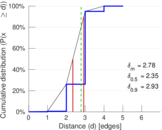


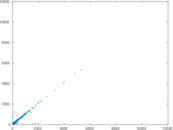
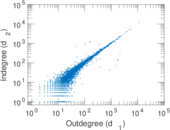
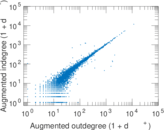
Matrix decompositions plots
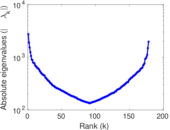
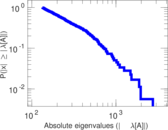
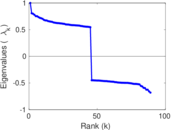
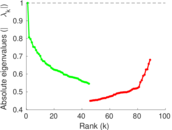
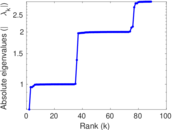
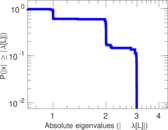
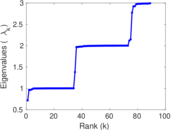

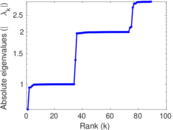
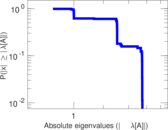
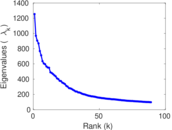
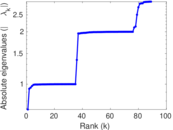
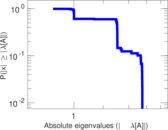
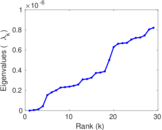

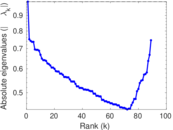
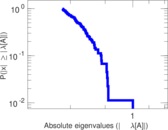
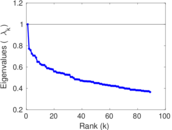
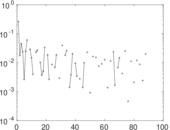
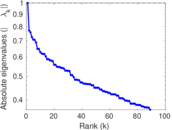
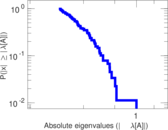
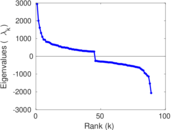
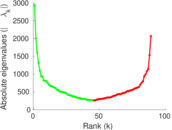
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Jure Leskovec.
Stanford Network Analysis Project.
http://snap.stanford.edu/, September 2014.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee