BookCrossing (implicit)

This network contains information about books read by members of the BookCrossing community. Nodes of the network are users and books, and an edge denotes that a user has interacted with a book.

Metadata

CodeBX
Internal namebookcrossing_full-rating
NameBookCrossing (implicit)
Data sourcehttp://www.informatik.uni-freiburg.de/~cziegler/BX/
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Interaction network
Dataset timestamp 2004-08-01 ⋯ 2004-09-01
Node meaningUser, book
Edge meaningRating
Network formatBipartite, undirected
Edge typeUnweighted, no multiple edges

Statistics

Size n =445,801
Left size n1 =105,278
Right size n2 =340,523
Volume m =1,149,739
Wedge count s =465,125,366
Claw count z =751,050,106,734
Cross count x =1,817,486,272,201,908
Square count q =93,843,300
4-Tour count T4 =2,613,565,786
Maximum degree dmax =13,601
Maximum left degree d1max =13,601
Maximum right degree d2max =2,502
Average degree d =5.158 08
Average left degree d1 =10.921 0
Average right degree d2 =3.376 39
Fill p =3.207 12 × 10−5
Size of LCC N =420,143
Diameter δ =19
50-Percentile effective diameter δ0.5 =4.118 29
90-Percentile effective diameter δ0.9 =5.781 38
Median distance δM =5
Mean distance δm =4.816 87
Gini coefficient G =0.752 201
Balanced inequality ratio P =0.196 535
Left balanced inequality ratio P1 =0.143 971
Right balanced inequality ratio P2 =0.264 016
Relative edge distribution entropy Her =0.854 894
Tail power law exponent γt =2.051 00
Tail power law exponent with p γ3 =2.051 00
p-value p =0.000 00
Left tail power law exponent with p γ3,1 =1.831 00
Left p-value p1 =0.000 00
Right tail power law exponent with p γ3,2 =2.141 00
Right p-value p2 =0.000 00
Degree assortativity ρ =−0.057 574 8
Degree assortativity p-value pρ =0.000 00
Spectral norm α =147.958
Algebraic connectivity a =0.010 442 0
Spectral separation |λ1[A] / λ2[A]| =1.466 78
Controllability C =295,185
Relative controllability Cr =0.662 145

Plots

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Delaunay graph drawing

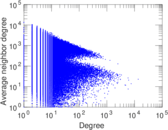
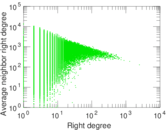
Matrix decompositions plots

Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Cai-Nicolas Ziegler, Sean M. McNee, Joseph A. Konstan, and Georg Lausen. Improving recommendation lists through topic diversification. In Proc. Int. World Wide Web Conf., pages 22–32, 2005.