Wikipedia edits (sh)
This is the bipartite edit network of the Serbo-Croatian Wikipedia. It contains
users and pages from the Serbo-Croatian Wikipedia, connected by edit events.
Each edge represents an edit. The dataset includes the timestamp of each edit.
Metadata
Statistics
| Size | n = | 4,589,850
|
| Left size | n1 = | 10,036
|
| Right size | n2 = | 4,579,814
|
| Volume | m = | 40,578,944
|
| Unique edge count | m̿ = | 6,265,053
|
| Wedge count | s = | 8,365,729,323,821
|
| Claw count | z = | 1.103 73 × 1019
|
| Cross count | x = | 1.113 82 × 1025
|
| Maximum degree | dmax = | 20,737,217
|
| Maximum left degree | d1max = | 20,737,217
|
| Maximum right degree | d2max = | 4,419
|
| Average degree | d = | 17.682 0
|
| Average left degree | d1 = | 4,043.34
|
| Average right degree | d2 = | 8.860 39
|
| Fill | p = | 0.000 136 306
|
| Average edge multiplicity | m̃ = | 6.477 03
|
| Size of LCC | N = | 4,587,753
|
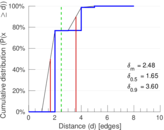
| Diameter | δ = | 10
|
| 50-Percentile effective diameter | δ0.5 = | 1.651 27
|
| 90-Percentile effective diameter | δ0.9 = | 3.599 44
|
| Median distance | δM = | 2
|
| Mean distance | δm = | 2.476 24
|
| Gini coefficient | G = | 0.922 198
|
| Balanced inequality ratio | P = | 0.062 076 3
|
| Left balanced inequality ratio | P1 = | 0.003 537 72
|
| Right balanced inequality ratio | P2 = | 0.102 502
|
| Degree assortativity | ρ = | −0.479 472
|
| Degree assortativity p-value | pρ = | 0.000 00
|
| Algebraic connectivity | a = | 0.032 412 4
|
Plots
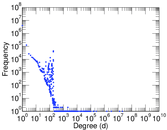
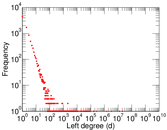
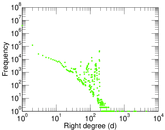
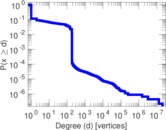
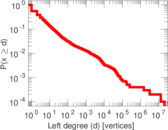
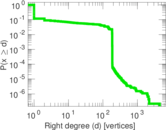
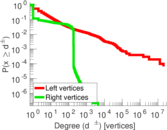
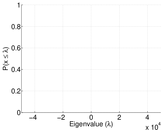
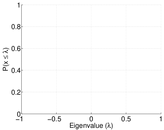
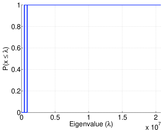
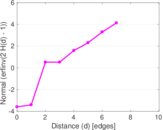
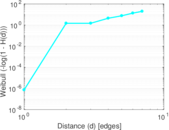
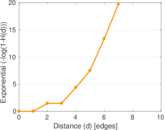
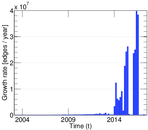
Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Wikimedia Foundation.
Wikimedia downloads.
http://dumps.wikimedia.org/, January 2010.
|
KONECT ‣ Networks ‣
Buy Me a Coffee
