FilmTrust ratings

This is bipartite rating network of the FilmTrust project. We removed three instances of duplicate user–film pairs; making the network simple rather than having multiple edges.

Metadata

CodeFR
Internal namelibrec-filmtrust-ratings
NameFilmTrust ratings
Data sourcehttps://www.librec.net/datasets.html
AvailabilityDataset is available for download
Consistency checkDataset passed all tests
Category
Rating network
Dataset timestamp 2011
Node meaningUser, film
Edge meaningRating
Network formatBipartite, undirected
Edge typeRatings, no multiple edges
Snapshot Is a snapshot and likely to not contain all data

Statistics

Size n =3,579
Left size n1 =1,508
Right size n2 =2,071
Volume m =35,494
Wedge count s =9,820,232
Claw count z =2,067,481,321
Cross count x =376,620,963,773
Square count q =99,312,706
4-Tour count T4 =833,882,216
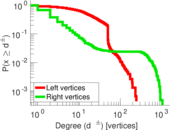
Maximum degree dmax =1,044
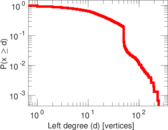
Maximum left degree d1max =244
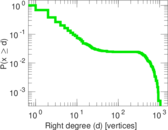
Maximum right degree d2max =1,044
Average degree d =19.834 6
Average left degree d1 =23.537 1
Average right degree d2 =17.138 6
Fill p =0.011 365 1
Size of LCC N =3,574
Diameter δ =7
50-Percentile effective diameter δ0.5 =2.739 74
90-Percentile effective diameter δ0.9 =3.839 54
Median distance δM =3
Mean distance δm =3.255 39
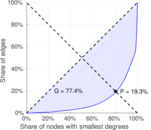
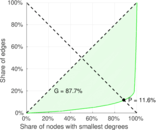
Gini coefficient G =0.716 391
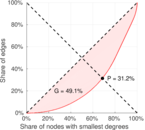
Balanced inequality ratio P =0.232 969
Left balanced inequality ratio P1 =0.312 194
Right balanced inequality ratio P2 =0.116 076
Relative edge distribution entropy Her =0.811 239
Power law exponent γ =1.605 27
Tail power law exponent γt =1.601 00
Tail power law exponent with p γ3 =1.601 00
p-value p =0.000 00
Left tail power law exponent with p γ3,1 =3.181 00
Left p-value p1 =0.218 000
Right tail power law exponent with p γ3,2 =2.061 00
Right p-value p2 =0.000 00
Degree assortativity ρ =−0.450 722
Degree assortativity p-value pρ =0.000 00
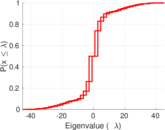
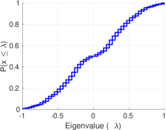
Spectral norm α =45.347 7
Algebraic connectivity a =0.007 217 86
Spectral separation |λ1[A] / λ2[A]| =1.343 74
Negativity ζ =0.439 736
Algebraic conflict ξ =0.267 701
Spectral signed frustration φ =0.003 369 74
Controllability C =2,478
Relative controllability Cr =0.692 372

Plots

Fruchterman–Reingold graph drawing

Degree distribution

Cumulative degree distribution

Lorenz curve

Spectral distribution of the adjacency matrix

Spectral distribution of the normalized adjacency matrix

Spectral distribution of the Laplacian

Spectral graph drawing based on the adjacency matrix

Spectral graph drawing based on the Laplacian

Spectral graph drawing based on the normalized adjacency matrix

Degree assortativity

Zipf plot

Hop distribution

Double Laplacian graph drawing

Delaunay graph drawing

Item rating evolution

Edge weight/multiplicity distribution

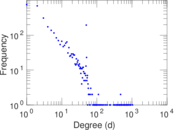
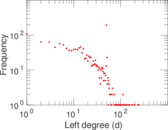
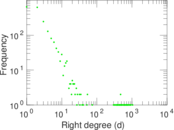
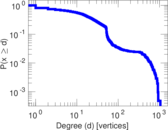
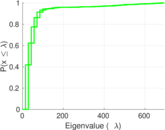
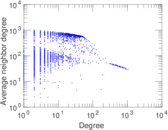
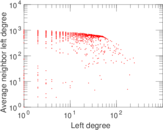
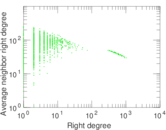
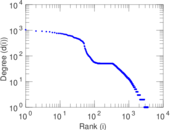
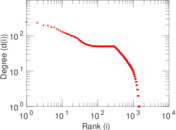
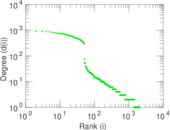
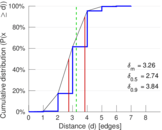
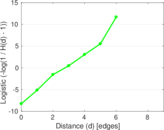
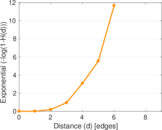
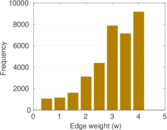
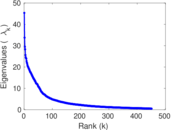
Matrix decompositions plots

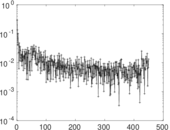
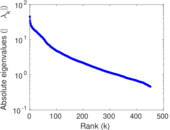
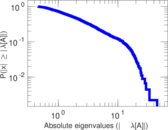
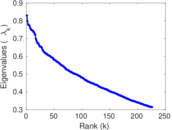
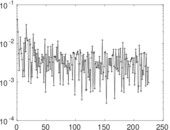
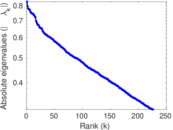
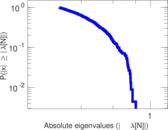
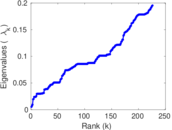
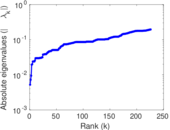
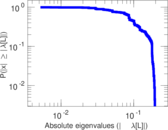
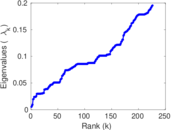
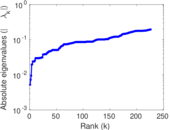
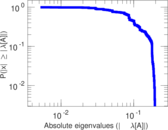
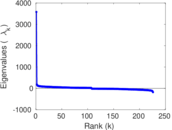
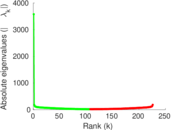
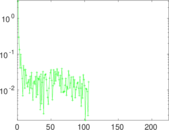
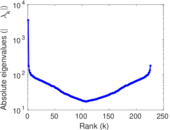
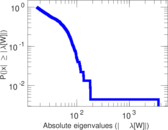
Downloads

References

[1] Jérôme Kunegis. KONECT – The Koblenz Network Collection. In Proc. Int. Conf. on World Wide Web Companion, pages 1343–1350, 2013. [ http ]
[2] Guobing Guo, Jia Zhang, and Neil Yorke-Smith. A novel Bayesian similarity measure for recommender systems. In Proc. Int. Joint Conf. on Artif. Intell., pages 2619–2625, 2013.