Crisis in a Cloister
This directed network contains ratings between monks related to a crisis in a
cloister (or monastery) in New England (USA) which lead to the departure of
several of the monks. This dataset aggregates several available ratings
((dis)esteem, (dis)liking, positive/negative influence, praise/blame) into only
one rating, which is positive if all original ratings were positive and
negative if all original ratings were negative. If there were mixed opinions
the rating has the value 0. A node represents a monk and an edge between two
monks shows that the left monk rated the right monk.
Metadata
Statistics
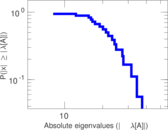
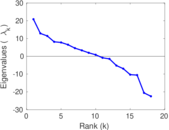
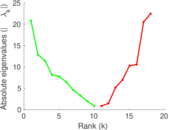
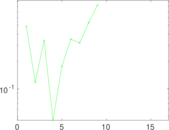
Plots

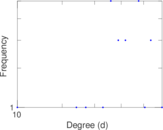
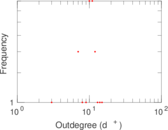
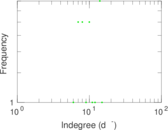
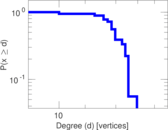
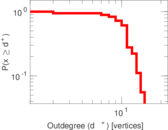
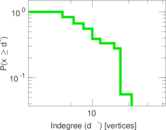
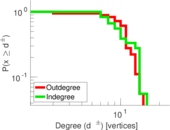
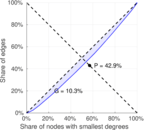
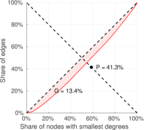
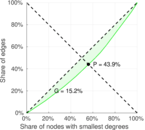
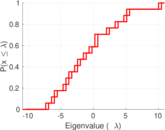
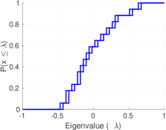
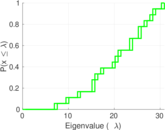





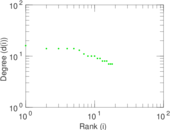
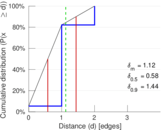
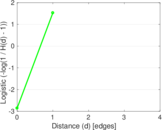
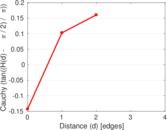

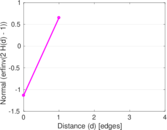
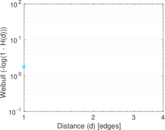
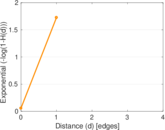





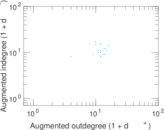
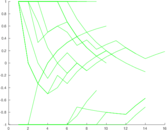
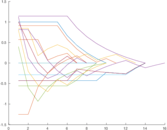
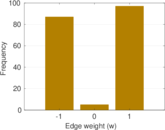
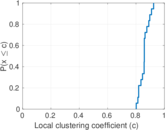
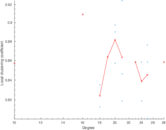

Matrix decompositions plots

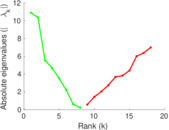





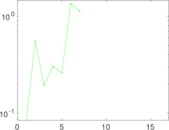


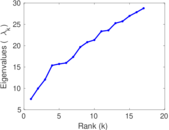
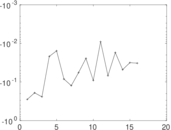
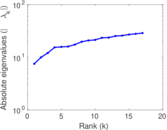
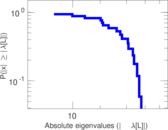
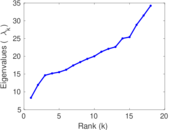
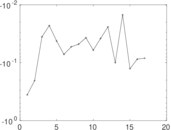

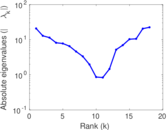
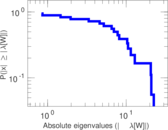
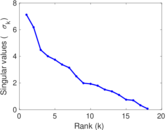
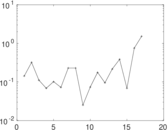



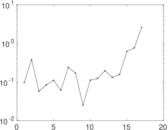
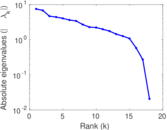

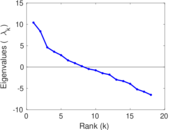


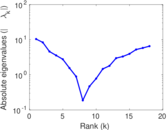
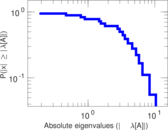

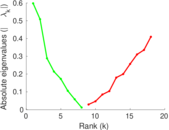
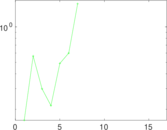
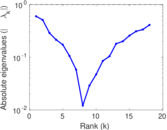
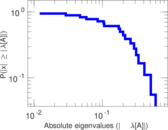
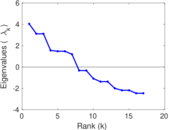
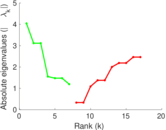
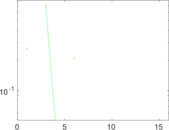
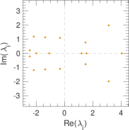
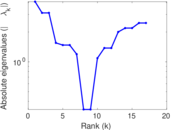

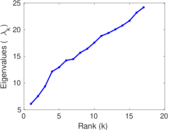
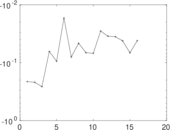

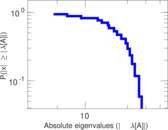

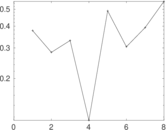
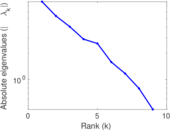
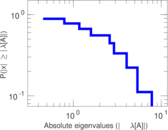
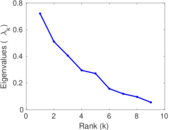
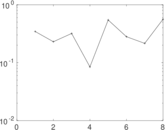
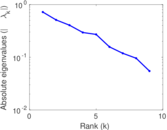
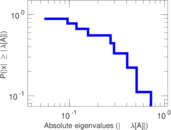
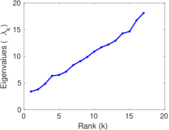
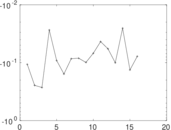
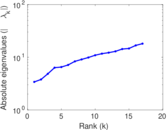
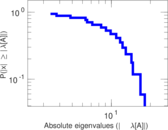

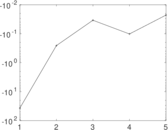
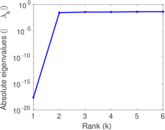
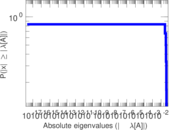

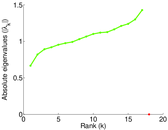

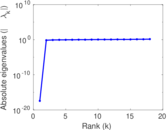
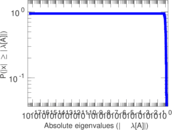
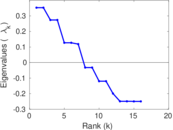
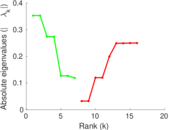
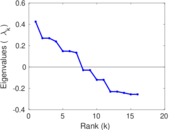
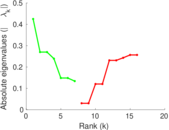
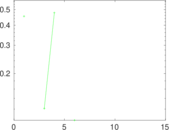
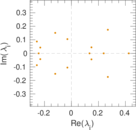
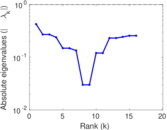
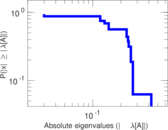
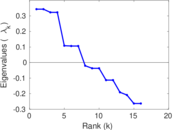
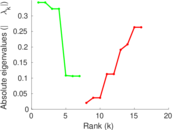


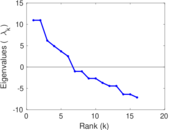
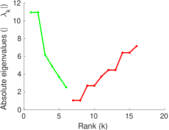

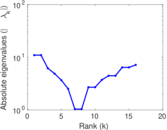
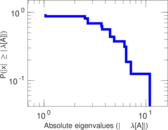

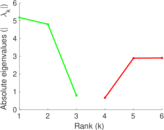
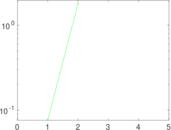
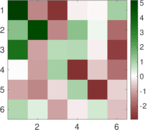
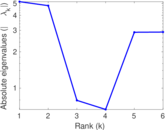
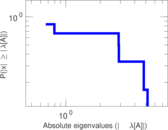
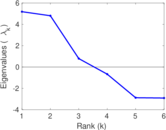
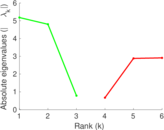
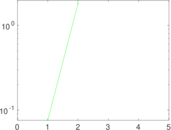
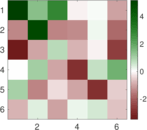

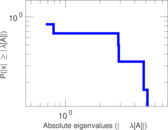
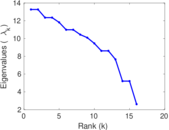
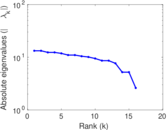

Downloads
References
|
[1]
|
Jérôme Kunegis.
KONECT – The Koblenz Network Collection.
In Proc. Int. Conf. on World Wide Web Companion, pages
1343–1350, 2013.
[ http ]
|
|
[2]
|
Ronald L. Breiger, Scott A. Boorman, and Phipps Arabie.
An algorithm for clustering relational data with applications to
social network analysis and comparison with multidimensional scaling.
J. of Math. Psychol., 12(3):328–383, 1975.
|
|
[3]
|
Samuel F. Sampson.
Crisis in a Cloister.
PhD thesis, Cornell Univ., 1969.
|
 KONECT ‣ Networks ‣
Buy Me a Coffee
KONECT ‣ Networks ‣
Buy Me a Coffee































































































































































